![\lim_{x\rightarrow3} \frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/5f39f5efab78062ec6e0b8dc308946ec.png "\lim_{x\rightarrow3} \frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}")
![a=\sqrt[3]{x}](/latexrender/pictures/be5c8af9ee83fbaa01f11dd8a49dcb17.png "a=\sqrt[3]{x}")
<=> 
![b=\sqrt[3]{3}](/latexrender/pictures/1a4d56d273021544fcd96aaaeeddb34d.png "b=\sqrt[3]{3}")
<=> 
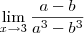
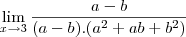
![\frac{1}{\sqrt[3]{3}^2 + \sqrt[3]{3}. \sqrt[3]{3} + \sqrt[3]{3}^2}](/latexrender/pictures/ee21fb5ebbe6d6242a194d98078782df.png "\frac{1}{\sqrt[3]{3}^2 + \sqrt[3]{3}. \sqrt[3]{3} + \sqrt[3]{3}^2}")
![\frac{1}{3.\sqrt[3]{3}^2}](/latexrender/pictures/ce5a1b6eeccc19b5aca008d9221b40cc.png "\frac{1}{3.\sqrt[3]{3}^2}")
???Esta certo issu??
por MarceloFantini » Qui Ago 12, 2010 21:40
por jcanutos » Seg Ago 16, 2010 12:17
por MarceloFantini » Seg Ago 16, 2010 22:56
![\lim_{x \to 0} \frac{\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/3bdee8abcfdfdb23b9095339dbd40847.png "\lim_{x \to 0} \frac{\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}")
![\frac{\sqrt[3]{3}}{3}](/latexrender/pictures/118ec34f59f09b53ca5838763eafaef8.png "\frac{\sqrt[3]{3}}{3}")
, o que já contradiz o resultado do seu limite supostamente certo. Agora, com o limite que você deveria ter escrito:![\lim_{x \to 3} \frac{\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/95ab1fa4805d9aaad444374333ea4c12.png "\lim_{x \to 3} \frac{\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}")
![\lim_{x \to 0} \frac{(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3)}{(x - 3)(x+3)} = \frac{\sqrt[3]{x \cdot x} - \sqrt[3]{3 \cdot x} + \sqrt[3]{3 \cdot x} - \sqrt[3]{3 \cdot 3}}{x^2 - 9} = \frac{\sqrt[3]{x^2} - \sqrt[3]{3^2}}{(x-3)(x+3)}](/latexrender/pictures/63dab3db2ef2da5d926dd430c3a3733e.png "\lim_{x \to 0} \frac{(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3)}{(x - 3)(x+3)} = \frac{\sqrt[3]{x \cdot x} - \sqrt[3]{3 \cdot x} + \sqrt[3]{3 \cdot x} - \sqrt[3]{3 \cdot 3}}{x^2 - 9} = \frac{\sqrt[3]{x^2} - \sqrt[3]{3^2}}{(x-3)(x+3)}")
![(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3) = x \sqrt[3]{x} - x \sqrt[3]{3} - 3 \sqrt[3]{x} + 3 \sqrt[3]{3}](/latexrender/pictures/7e29cb9b77c2d32c95fae6fcb025f6eb.png "(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3) = x \sqrt[3]{x} - x \sqrt[3]{3} - 3 \sqrt[3]{x} + 3 \sqrt[3]{3}")
![(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3) \neq \sqrt[3]{x \cdot x} - \sqrt[3]{3 \cdot x} + \sqrt[3]{3 \cdot x} - \sqrt[3]{3 \cdot 3} = \sqrt[3]{x^2} - \sqrt[3]{3^2}](/latexrender/pictures/41df97bc5fa0200d27f525af35dd2f64.png "(\sqrt[3]{x} - \sqrt[3]{3}) \cdot (x+3) \neq \sqrt[3]{x \cdot x} - \sqrt[3]{3 \cdot x} + \sqrt[3]{3 \cdot x} - \sqrt[3]{3 \cdot 3} = \sqrt[3]{x^2} - \sqrt[3]{3^2}")
![\frac{\sqrt[3]{x^2} - \sqrt[3]{3^2}}{(x-3)(x+3)} = \frac{1^{\frac{2}{3}}(x - 3)}{(x-3)(x+3)} = \frac{\sqrt[3]{1^2}}{x+3} = \frac{1}{6}](/latexrender/pictures/02c963f3cbe37f52d76327085050d528.png "\frac{\sqrt[3]{x^2} - \sqrt[3]{3^2}}{(x-3)(x+3)} = \frac{1^{\frac{2}{3}}(x - 3)}{(x-3)(x+3)} = \frac{\sqrt[3]{1^2}}{x+3} = \frac{1}{6}")
![\sqrt[3]{1^2}](/latexrender/pictures/9a1bac8a5f1aa77f80b73b5c1d112a0d.png "\sqrt[3]{1^2}")
em evidência e SUMIU (???) com as potências de 
e 
(tudo isso, claro, sem escrever limite, o que continua demonstrando a dedução de uma conta sem sentido algum), levando ao resultado fantástico de que ![\sqrt[3]{1^2} = 1](/latexrender/pictures/109ee31b7569cba1842c02b861b14df3.png "\sqrt[3]{1^2} = 1")
(uau, obrigado, não sabia dessa...) e substituiu por 3 (peraí, o limite não era tendendo à zero?), levando ao resultado final de 
.Voltar para Cálculo: Limites, Derivadas e Integrais
por Raphaela_sf » Qui Abr 05, 2012 19:26
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a e elevar ao quadrado os dois lados)![\lim_{X\rightarrow0}\frac{\sqrt[3]{X}-\sqrt[3]{3}}{X-3}= \frac{\sqrt[3]{X}-\sqrt[3]{3}.(X+3)}{X-3 . (X+3)}= \frac{\sqrt[3]{X.X}-\sqrt[3]{3.X}+\sqrt[3]{3.X}-\sqrt[3]{3.3}}{{X}^{2}-3.X+3.X-{3}^{2}}= \frac{\sqrt[3]{{X}^{2}}-\sqrt[3]{{3}^{2}}}{{X}^{2}-{3}^{2}}= \frac{X.{1}^{\frac{2}{3}}-3.{1}^{\frac{2}{3}}}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}.(X-3)}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}}{X+3}= \frac{\sqrt[3]{{1}^{2}}}{6} = \frac{1}{6}](/latexrender/pictures/06a4cfd4346d91759493b62b7d7df284.png "\lim_{X\rightarrow0}\frac{\sqrt[3]{X}-\sqrt[3]{3}}{X-3}= \frac{\sqrt[3]{X}-\sqrt[3]{3}.(X+3)}{X-3 . (X+3)}= \frac{\sqrt[3]{X.X}-\sqrt[3]{3.X}+\sqrt[3]{3.X}-\sqrt[3]{3.3}}{{X}^{2}-3.X+3.X-{3}^{2}}= \frac{\sqrt[3]{{X}^{2}}-\sqrt[3]{{3}^{2}}}{{X}^{2}-{3}^{2}}= \frac{X.{1}^{\frac{2}{3}}-3.{1}^{\frac{2}{3}}}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}.(X-3)}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}}{X+3}= \frac{\sqrt[3]{{1}^{2}}}{6} = \frac{1}{6}")
![\lim_{X\rightarrow3}\frac{\sqrt[3]{X}-\sqrt[3]{3}}{X-3}= \frac{(\sqrt[3]{X}-\sqrt[3]{3}).(X+3)}{X-3 . (X+3)}= \frac{\sqrt[3]{X.X}-\sqrt[3]{3.X}+\sqrt[3]{3.X}-\sqrt[3]{3.3}}{{X}^{2}-3.X+3.X-{3}^{2}}= \frac{\sqrt[3]{{X}^{2}}-\sqrt[3]{{3}^{2}}}{{X}^{2}-{3}^{2}}= \frac{X.{1}^{\frac{2}{3}}-3.{1}^{\frac{2}{3}}}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}.(X-3)}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}}{X+3}= \frac{\sqrt[3]{{1}^{2}}}{6} = \frac{1}{6}](/latexrender/pictures/4622d32dfc53426d66da1f3b8a1c4bfc.png "\lim_{X\rightarrow3}\frac{\sqrt[3]{X}-\sqrt[3]{3}}{X-3}= \frac{(\sqrt[3]{X}-\sqrt[3]{3}).(X+3)}{X-3 . (X+3)}= \frac{\sqrt[3]{X.X}-\sqrt[3]{3.X}+\sqrt[3]{3.X}-\sqrt[3]{3.3}}{{X}^{2}-3.X+3.X-{3}^{2}}= \frac{\sqrt[3]{{X}^{2}}-\sqrt[3]{{3}^{2}}}{{X}^{2}-{3}^{2}}= \frac{X.{1}^{\frac{2}{3}}-3.{1}^{\frac{2}{3}}}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}.(X-3)}{(X-3).(X+3)}= \frac{{1}^{\frac{2}{3}}}{X+3}= \frac{\sqrt[3]{{1}^{2}}}{6} = \frac{1}{6}")