 por LUCKYSB » Qua Jun 02, 2010 20:16
por LUCKYSB » Qua Jun 02, 2010 20:16
ITA-SP) Dentro de um tronco de pirâmide quadrangular regular, considera-se uma pirâmide regular cuja base é a base maior do tronco e cujo vértice é o centro da base menor do tronco. As arestas das bases medem a cm e 2acm. As áreas laterais do tronco e da pirâmide são iguais. Calcular a altura do tronco da pirâmide.
-
LUCKYSB
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 02, 2010 19:56
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: matematica
- Andamento: cursando
 por Douglasm » Qua Jun 02, 2010 20:54
por Douglasm » Qua Jun 02, 2010 20:54
Olá LUCKYSB. Para resolver esse problema eu vou contar com a sua visão da figura em 3 dimensões, pois eu só vou postar os desenhos necessários para explicar os apótemas. Então vamos lá:
Primeiramente vamos a algumas considerações:

= aresta menor do tronco

= aresta maior do tronco

= altura
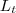
= apótema do tronco
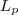
= apótema da pirâmide

= área lateral do tronco

= área lateral da pirâmide
Para resolver o problema basta exprimirmos as áreas laterais em função de
a e
h. Comecemos com a área lateral do tronco:
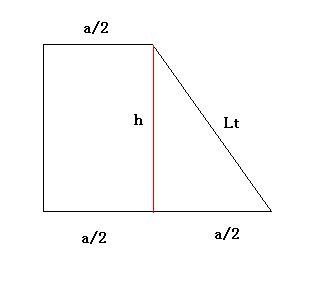
- apótema tronco.jpg (6.13 KiB) Exibido 3445 vezes

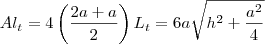
Para a pirâmide:

- apótema pirâmide.jpg (5.08 KiB) Exibido 3445 vezes


Igualando as duas áreas:


Elevamos ambos os membros ao quadrado:


Até a próxima.
Editado pela última vez por
Douglasm em Qua Jun 02, 2010 22:09, em um total de 2 vezes.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LUCKYSB » Qua Jun 02, 2010 20:59
por LUCKYSB » Qua Jun 02, 2010 20:59
muito obrigado por ajudar grato
-
LUCKYSB
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jun 02, 2010 19:56
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6390 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3674 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2895 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2287 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4422 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 = aresta menor do tronco
= aresta menor do tronco  = aresta maior do tronco
= aresta maior do tronco  = altura
= altura 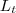 = apótema do tronco
= apótema do tronco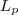 = apótema da pirâmide
= apótema da pirâmide = área lateral do tronco
= área lateral do tronco = área lateral da pirâmide
= área lateral da pirâmide
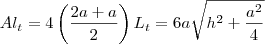









 .
.



