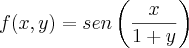
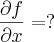
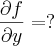
e a derivada parcial da outra função:

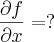
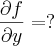
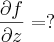
Alguém pode me ajudar?
Grato
José Mario

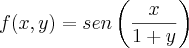
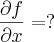
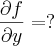

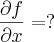
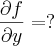
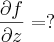

![f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y} f(x,y) = sen \left(\frac{x}{1+y}\right) \; \therefore \; \frac{\partial \left[sen \left(\frac{x}{1+y}\right)\right]}{\partial x} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{1}{1+y}](/latexrender/pictures/fe6284eedc4b9d6ad5cf3623de5ab1c0.png)

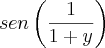
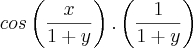

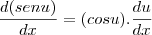
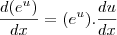
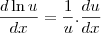
![\frac{\partial f}{\partial y} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{-x}{(1+y)^2} \frac{\partial f}{\partial y} = \left[cos\left(\frac{x}{1+y}\right)\right] . \frac{-x}{(1+y)^2}](/latexrender/pictures/ba5f9d05fa5ddfcb49a66afae2971167.png)
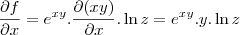
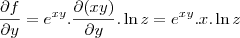
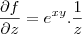


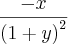
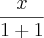

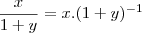
![\frac{\partial \left[\frac{x}{1+y}\right]}{\partial y} = \frac{\partial \left[x . (1+y)^{-1}\right]}{\partial y} = \frac{\partial \left[\frac{x}{1+y}\right]}{\partial y} = \frac{\partial \left[x . (1+y)^{-1}\right]}{\partial y} =](/latexrender/pictures/d5c9767d3bca2e5977e38dbe1bf31d0e.png)
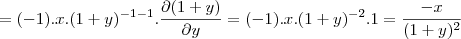

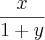 vira
vira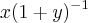

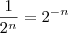
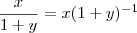

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)