 por lunayanne » Dom Mar 07, 2010 00:15
por lunayanne » Dom Mar 07, 2010 00:15
-
lunayanne
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mar 06, 2010 23:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por ogoiD » Sáb Mar 27, 2010 23:07
por ogoiD » Sáb Mar 27, 2010 23:07
Na primeira e terceira , é só voce fatorar e cancelar o divisor , depois substitui o valor
-
ogoiD
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Mar 22, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecanica
- Andamento: cursando
 por lucas92 » Ter Abr 13, 2010 03:57
por lucas92 » Ter Abr 13, 2010 03:57

A primeira, nem faço ideia de como se resolve.
A segunda, na verdade, é o limite da soma de n funções potências, observe:
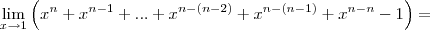
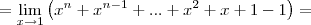
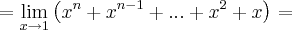


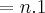
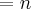
.
Na terceira, aplicando o limite, dá "0/0". Então, devemos primeiro, transformar os radicais para que eles tenham o mesmo índice:
![\lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} \lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}}](/latexrender/pictures/6d8b8b57d56a1bb727d2abbfc895c754.png)
Vamos fazer uma mudança de variável. Fazendo
![\sqrt[6]{x} = k \sqrt[6]{x} = k](/latexrender/pictures/ed9facde3b125cd8c99991c049f529b6.png)
, temos que
![\sqrt[6]{x^2} = k^2 \sqrt[6]{x^2} = k^2](/latexrender/pictures/18f69ff7d550e3a6e09e7ed55e3da404.png)
e
![\sqrt[6]{x^3} = k^3 \sqrt[6]{x^3} = k^3](/latexrender/pictures/1904f6b30e514f0d8fa5e66eb299183d.png)
. E se
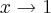
, então
![k\rightarrow\sqrt[3]{1} = 1 k\rightarrow\sqrt[3]{1} = 1](/latexrender/pictures/145c29c1ac9a425e368d56dfa476eece.png)
. Aí ficamos com:
![\lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3} \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3}](/latexrender/pictures/41cbbf22a00ced820b847d82a78bb40f.png)
Aplicando novamente o limite, continua ainda a indeterminação "0/0". Mas agora nós temos um limite do quociente entre duas funções polinomiais. E se k=1 zera o polinômio do numerador e do denominador, então esses polinômios são divisíveis por

. Logo, temos:
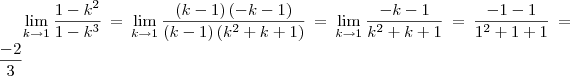
.
-
lucas92
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 09, 2010 06:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Limites exponenciais com euler.
por yuricastilho » Ter Abr 15, 2014 14:30
- 2 Respostas
- 2271 Exibições
- Última mensagem por yuricastilho

Qui Mai 01, 2014 16:28
Cálculo: Limites, Derivadas e Integrais
-
- limites exponenciais
por uefs » Qua Mai 14, 2014 18:36
- 1 Respostas
- 1389 Exibições
- Última mensagem por e8group

Qui Mai 15, 2014 02:23
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES de exponenciais e logaritimos
por inkz » Qua Dez 05, 2012 16:13
- 1 Respostas
- 1686 Exibições
- Última mensagem por e8group

Qua Dez 05, 2012 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Exponenciais
por Souo » Ter Jun 30, 2015 01:42
- 3 Respostas
- 2691 Exibições
- Última mensagem por nakagumahissao

Sex Jul 03, 2015 21:24
Logaritmos
-
- Exponenciais
por Souo » Sáb Jun 20, 2015 14:45
- 1 Respostas
- 1754 Exibições
- Última mensagem por Cleyson007

Dom Jun 21, 2015 09:20
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} \lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}}](/latexrender/pictures/95767d850ccd39bf08d6540052a72c3f.png)




![\lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} \lim_{x\rightarrow1}\frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}}](/latexrender/pictures/95767d850ccd39bf08d6540052a72c3f.png)




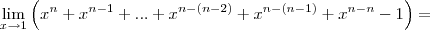
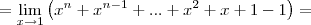
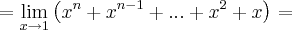


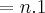
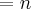 .
.![\lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} \lim_{x\rightarrow1} \frac{1-\sqrt[3]{x}}{1-\sqrt[2]{x}} = \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}}](/latexrender/pictures/6d8b8b57d56a1bb727d2abbfc895c754.png)
![\sqrt[6]{x} = k \sqrt[6]{x} = k](/latexrender/pictures/ed9facde3b125cd8c99991c049f529b6.png) , temos que
, temos que ![\sqrt[6]{x^2} = k^2 \sqrt[6]{x^2} = k^2](/latexrender/pictures/18f69ff7d550e3a6e09e7ed55e3da404.png) e
e ![\sqrt[6]{x^3} = k^3 \sqrt[6]{x^3} = k^3](/latexrender/pictures/1904f6b30e514f0d8fa5e66eb299183d.png) . E se
. E se 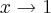 , então
, então ![k\rightarrow\sqrt[3]{1} = 1 k\rightarrow\sqrt[3]{1} = 1](/latexrender/pictures/145c29c1ac9a425e368d56dfa476eece.png) . Aí ficamos com:
. Aí ficamos com:![\lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3} \lim_{x\rightarrow1} \frac{1-\sqrt[6]{x^2}}{1-\sqrt[6]{x^3}} = \lim_{k\rightarrow1} \frac{1-k^2}{1-k^3}](/latexrender/pictures/41cbbf22a00ced820b847d82a78bb40f.png)
 . Logo, temos:
. Logo, temos: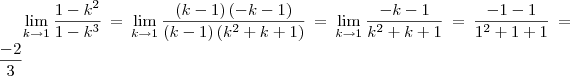 .
.





