 por lucas92 » Sex Abr 09, 2010 07:21
por lucas92 » Sex Abr 09, 2010 07:21
Oi, gente. Eu estava aqui tentando calcular esse limite:
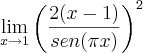
Encontrei zero como resultado baseado em esse ser um limite do produto de uma função limitada envolvendo seno,
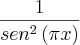
, por uma infinitésima cujo limite vai a zero,
![{\left[2\left(x-1 \right) \right]}^{2} {\left[2\left(x-1 \right) \right]}^{2}](/latexrender/pictures/6a713ab7063e6073d745a9a6f86e1fb9.png)
. Só que para minha surpresa, no gabarito a resposta é
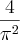
. Como eu chegaria a essa resposta? Não faço a mínima ideia.
Obrigado
-
lucas92
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 09, 2010 06:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação
- Andamento: cursando
 por Neperiano » Sex Abr 09, 2010 11:03
por Neperiano » Sex Abr 09, 2010 11:03
Ola
lucas92 escreveu:Oi, gente. Eu estava aqui tentando calcular esse limite:
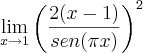
Encontrei zero como resultado baseado em esse ser um limite do produto de uma função limitada envolvendo seno,
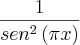
, por uma infinitésima cujo limite vai a zero,
![{\left[2\left(x-1 \right) \right]}^{2} {\left[2\left(x-1 \right) \right]}^{2}](/latexrender/pictures/6a713ab7063e6073d745a9a6f86e1fb9.png)
. Só que para minha surpresa, no gabarito a resposta é
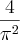
. Como eu chegaria a essa resposta? Não faço a mínima ideia.
Obrigado
Primeiro corte tudo o que pode, ficara
(2(-1))^2 emcima
(sen(pi)) embaixo
Multiplique emcima e embaixo
(-2)^2
(senpi)
4/pi^2,
Quanto ao seno acredito que ele desaparece, ainda não sei explicar porque mas pesquisarei, espero ter ajudado
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Neperiano » Sex Abr 09, 2010 11:07
por Neperiano » Sex Abr 09, 2010 11:07
Ola
Ja axei
Lim sen(x)/x = 1
x-0
Ou seja no momento em quer cortar o x na questão automaticamente corte o seno tambem, o resultado sera 1
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Douglasm » Dom Abr 11, 2010 16:39
por Douglasm » Dom Abr 11, 2010 16:39
Olá lucas92. Para encontrar o limite abaixo, eu usei a
regra de L'Hopital (assunto estudado em derivadas, caso haja duvidas sobre o método é só consultar um livro de cálculo). Comecemos:
Podemos observar que:
![\lim_{x\rightarrow 1} [2(x-1)]^2 = 0 \lim_{x\rightarrow 1} [2(x-1)]^2 = 0](/latexrender/pictures/c19f117c05ecb459a3a05058f61d382a.png)
;
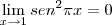
Essas são as condições necessárias para aplicarmos a regra de L'Hopital, e devemos agora derivar as equações (as derivamos separadamente, não utilizamos aqui a regra do quociente), mas primeiro vamos arrumá-las:
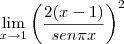

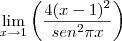
Comecemos a derivar:
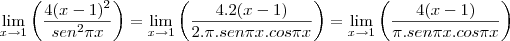
Agora vamos derivar mais uma vez (é importante prestar bastante atenção na derivada da função seno acima e na próxima em que deveremos aplicar a regra do produto):
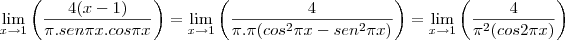
Finalmente:
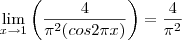
Obs: É importante lembrar que para podermos continuar derivando como fizemos nesse exercício a 1ª condição (a de que f(x)/g(x) seja uma indeterminação) seja satisfeita também para a derivada, como é o caso aqui.
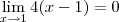
;
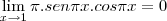
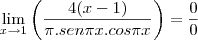
Caso tenha dúvidas sobre algum procedimento usado, me diga! Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lucas92 » Seg Abr 12, 2010 03:06
por lucas92 » Seg Abr 12, 2010 03:06
Oi gente, já consegui resolver o problema. Não fiz nada além de trocar a variável. Como o limite envolve uma função trigonométrica, temos que destrinchar esse limite par que apareça o limite trigonométrico fundamental:
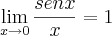
.
Como no problema, a variável não tende a zero, tende a 1, vamos transformar a varíável x.
Fazendo
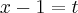
, temos que
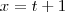
. E se
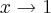
, então
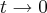
. Substituindo

por

, e

por

, ficamos com:
![\lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} = \lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} =](/latexrender/pictures/a84fa756da823cceeed5cae020618f78.png)
![=\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} = =\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} =](/latexrender/pictures/7c7520eaebb9360046cbdfc1d121ba97.png)
![=\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}} =\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}}](/latexrender/pictures/52829ff3c16e0a8b4602b13a92a8db1e.png)
.
Valeu para quem me ajudou.
-
lucas92
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 09, 2010 06:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação
- Andamento: cursando
 por Douglasm » Seg Abr 12, 2010 10:32
por Douglasm » Seg Abr 12, 2010 10:32
Olá lucas92. Olhei sua resolução e não entendi o último passo:
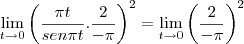
O resultado seria a indeterminação

(que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é
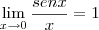
e não
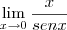
(se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso?
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por lucas92 » Ter Abr 13, 2010 01:13
por lucas92 » Ter Abr 13, 2010 01:13
Douglasm escreveu:Olá lucas92. Olhei sua resolução e não entendi o último passo:
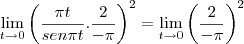
O resultado seria a indeterminação

(que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é
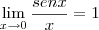
e não
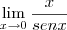
(se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso?
Até a próxima.
Realmente, quando calculei esse limite
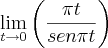
subentendi, que ele daria 1. Observe:
Vamos pensar assim: se
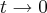
, então

, concorda? Aí ficamos com:
![\lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1 \lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1](/latexrender/pictures/9e18dd484cacc55ac20ac627096623cd.png)
.
Então, repare que eu não simplesmente "cortei" a indeterminação do nada, simplesmente, subentendi algumas passagens para o cálculo do limite que realmente é 1.
-
lucas92
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 09, 2010 06:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Computação
- Andamento: cursando
 por Douglasm » Ter Abr 13, 2010 10:10
por Douglasm » Ter Abr 13, 2010 10:10
Não havia me atentado a isso! Realmente está correto. Então do seu jeito ficou bem mais objetivo. =)
Bons estudos e até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5448 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de limites
por Hansegon » Seg Ago 25, 2008 11:29
- 2 Respostas
- 59836 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 16:03
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de limites
por Emanuel_27 » Sáb Nov 01, 2008 01:57
- 3 Respostas
- 7154 Exibições
- Última mensagem por Molina

Qui Abr 09, 2009 22:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
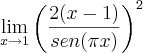
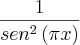 , por uma infinitésima cujo limite vai a zero,
, por uma infinitésima cujo limite vai a zero, ![{\left[2\left(x-1 \right) \right]}^{2} {\left[2\left(x-1 \right) \right]}^{2}](/latexrender/pictures/6a713ab7063e6073d745a9a6f86e1fb9.png) . Só que para minha surpresa, no gabarito a resposta é
. Só que para minha surpresa, no gabarito a resposta é 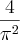 . Como eu chegaria a essa resposta? Não faço a mínima ideia.
. Como eu chegaria a essa resposta? Não faço a mínima ideia.


![\lim_{x\rightarrow 1} [2(x-1)]^2 = 0 \lim_{x\rightarrow 1} [2(x-1)]^2 = 0](/latexrender/pictures/c19f117c05ecb459a3a05058f61d382a.png) ;
; 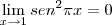
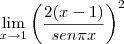

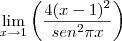
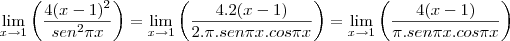
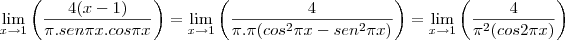
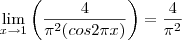
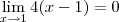 ;
; 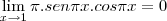
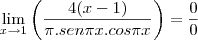
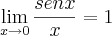 .
. 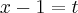 , temos que
, temos que 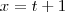 . E se
. E se 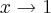 , então
, então 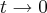 . Substituindo
. Substituindo  por
por  , e
, e  por
por  , ficamos com:
, ficamos com:![\lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} = \lim_{x\rightarrow1} {\left[\frac{2\left(x-1 \right)}{sen\left(\pi x \right)} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen\left[\pi \left(t+1 \right) \right] \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{sen \left(\pi t+\pi \right)} \right]}^{2} =](/latexrender/pictures/a84fa756da823cceeed5cae020618f78.png)
![=\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} = =\lim_{t\rightarrow0} {\left[\frac{2t}{sen \pi t.cos\pi+sen \pi .cos\pi t} \right]}^{2} = \lim_{t\rightarrow0} {\left[\frac{2t}{-sen\pi t} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2t.\pi}{\left(-sen\pi t \right).\pi} \right]^{2} =](/latexrender/pictures/7c7520eaebb9360046cbdfc1d121ba97.png)
![=\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}} =\lim_{t\rightarrow0} \left[\frac{2\pi t}{\left(-sen\pi t \right).\pi} \right]^{2} = \lim_{t\rightarrow0} {\left[\frac{\pi t}{sen \pi t} . \frac{2}{\left(-\pi \right)} \right]}^{2} = \lim_{t\rightarrow0} \left[\frac{2}{-\pi} \right]^2 = \frac{4}{{\pi}^{2}}](/latexrender/pictures/52829ff3c16e0a8b4602b13a92a8db1e.png) .
.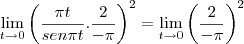
 (que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é
(que não pode ser simplesmente cortada). Se falares do limite trigonométrico fundamental, ele é 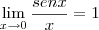 e não
e não 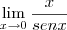 (se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso?
(se observar a definição do limite trigonométrico, verá como nesse caso a função não tende a 1). E então como é isso? 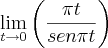
 , concorda? Aí ficamos com:
, concorda? Aí ficamos com:![\lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1 \lim_{t\rightarrow0} \left(\frac{\pi t}{sen\pi t} \right) = \lim_{\pi t\rightarrow0} \left(\frac{\pi t}{sen \pi t} \right) = \lim_{\pi t\rightarrow0} \left[\frac{1}{\frac{sen \pi t}{\pi t}} \right] = \frac{1}{1} = 1](/latexrender/pictures/9e18dd484cacc55ac20ac627096623cd.png) .
.




