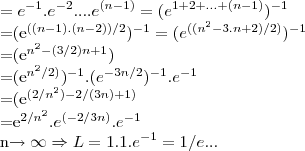por adauto martins » Seg Abr 12, 2021 15:59
por adauto martins » Seg Abr 12, 2021 15:59
(ITA-1952) calcular o
![\lim_{n\rightarrow\infty}\sqrt[n]{n!}/n \lim_{n\rightarrow\infty}\sqrt[n]{n!}/n](/latexrender/pictures/516fbc781b5ecbd5e20c5ecb3e48d7d1.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Seg Abr 12, 2021 17:04
por adauto martins » Seg Abr 12, 2021 17:04
soluçao
precisarei de dois argumentos para resolver esse exercicio
o limite fundamental
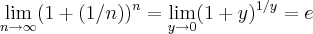
e o limite,que é consequencia do limite fundamental apresentado
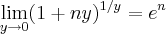
de fato,
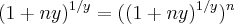
façamos
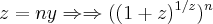
logo

voltemos a questao
![L=\sqrt[n]{n!}/n=\sqrt[n]{n!/n^{n}}=((n.(n-1)....2.1)/n^{n})^{1/n}
=((n/n).(n-1)/n....(2/n).(1/n))^{1/n}
=(1-1/n)^{1/n}.(1-2/n)^{1/n}
....(1-(n-2)/n)^{1/n}.(1-(n-1)/n)^{1/n} L=\sqrt[n]{n!}/n=\sqrt[n]{n!/n^{n}}=((n.(n-1)....2.1)/n^{n})^{1/n}
=((n/n).(n-1)/n....(2/n).(1/n))^{1/n}
=(1-1/n)^{1/n}.(1-2/n)^{1/n}
....(1-(n-2)/n)^{1/n}.(1-(n-1)/n)^{1/n}](/latexrender/pictures/7b48c61ca11a250ee37a3516d36c757e.png)
façamos

entao
![\sqrt[n]{n!}/n=(1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y}
\lim_{y\rightarrow0}((1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y})
(\lim_{y\rightarrow0}(1+y)^{-1/y})....(\lim_{y\rightarrow0}(1+(n-1)y)^{-(n-1)/y}) \sqrt[n]{n!}/n=(1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y}
\lim_{y\rightarrow0}((1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y})
(\lim_{y\rightarrow0}(1+y)^{-1/y})....(\lim_{y\rightarrow0}(1+(n-1)y)^{-(n-1)/y})](/latexrender/pictures/2b6affca442fc9b24cf49ad3d80b7bcb.png)
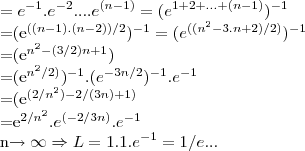
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 19931 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Qua Jul 20, 2016 18:35
- 0 Respostas
- 18336 Exibições
- Última mensagem por adauto martins

Qua Jul 20, 2016 18:35
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 8837 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 4382 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 8994 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{n\rightarrow\infty}\sqrt[n]{n!}/n \lim_{n\rightarrow\infty}\sqrt[n]{n!}/n](/latexrender/pictures/516fbc781b5ecbd5e20c5ecb3e48d7d1.png)


![\lim_{n\rightarrow\infty}\sqrt[n]{n!}/n \lim_{n\rightarrow\infty}\sqrt[n]{n!}/n](/latexrender/pictures/516fbc781b5ecbd5e20c5ecb3e48d7d1.png)

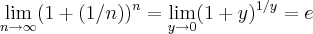
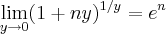
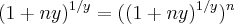
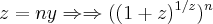

![L=\sqrt[n]{n!}/n=\sqrt[n]{n!/n^{n}}=((n.(n-1)....2.1)/n^{n})^{1/n}
=((n/n).(n-1)/n....(2/n).(1/n))^{1/n}
=(1-1/n)^{1/n}.(1-2/n)^{1/n}
....(1-(n-2)/n)^{1/n}.(1-(n-1)/n)^{1/n} L=\sqrt[n]{n!}/n=\sqrt[n]{n!/n^{n}}=((n.(n-1)....2.1)/n^{n})^{1/n}
=((n/n).(n-1)/n....(2/n).(1/n))^{1/n}
=(1-1/n)^{1/n}.(1-2/n)^{1/n}
....(1-(n-2)/n)^{1/n}.(1-(n-1)/n)^{1/n}](/latexrender/pictures/7b48c61ca11a250ee37a3516d36c757e.png)

![\sqrt[n]{n!}/n=(1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y}
\lim_{y\rightarrow0}((1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y})
(\lim_{y\rightarrow0}(1+y)^{-1/y})....(\lim_{y\rightarrow0}(1+(n-1)y)^{-(n-1)/y}) \sqrt[n]{n!}/n=(1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y}
\lim_{y\rightarrow0}((1+y)^{-1/y}.(1+2y)^{-2/y}....(1+(n-1)y)^{-(n-1)/y})
(\lim_{y\rightarrow0}(1+y)^{-1/y})....(\lim_{y\rightarrow0}(1+(n-1)y)^{-(n-1)/y})](/latexrender/pictures/2b6affca442fc9b24cf49ad3d80b7bcb.png)