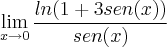
já tentei propriedades logarítmicas,multiplicar a fração por conjugados mas não chego a lugar nenhum.
Gab: 3

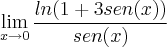

MCordeiro escreveu:Resolva sem utilizar L'hospital:
já tentei propriedades logarítmicas,multiplicar a fração por conjugados mas não chego a lugar nenhum.
Gab: 3
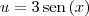
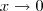 , teremos
, teremos  . Desse modo, o limite pode ser reescrito como:
. Desse modo, o limite pode ser reescrito como:
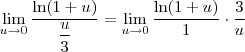
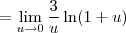
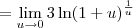
![= 3\ln \left[\lim_{u\to 0}(1 + u)^\frac{1}{u}\right] = 3\ln \left[\lim_{u\to 0}(1 + u)^\frac{1}{u}\right]](/latexrender/pictures/3120eefc34e780e448279799e16e60d7.png)



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)