Estou com dificuldades em resolver um limite.
é o seguinte:

entao, iniciei separando em duas frações, ambas com demoninador (x-1), fazendo os limites separados.
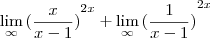
O segundo termo cheguei à conclusão que é 1/infinito=0
O primeiro termo conclui que a resposta do limite é e^2, após mudar a base e todo aquele processo de sempre, hehehehe, gostaria de saber se está correto, pois desconfio que não! kkkkkkkk


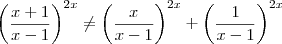
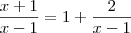 .
.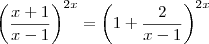
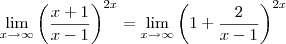 .
. 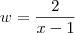 .Quando
.Quando 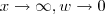 .Fazendo as substituições ,
.Fazendo as substituições , 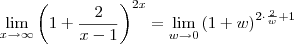
 e
e 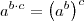 e também dos limites, uma delas do produto .
e também dos limites, uma delas do produto . ![\lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4 \lim_{w\to 0} \left(1 + w \right ) ^{2 \cdot \frac{2}{w} + 1} = \left[\lim_{w\to 0} \left(1 + w \right ) ^{1/w }\right]^4 \cdot \lim_{w\to 0} (1 + w) = e^4](/latexrender/pictures/0e2d8979072ad1690fa73549a2250b33.png) .
. 
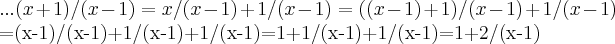

 .
.
 :
: