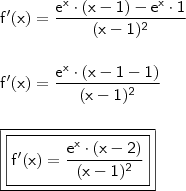por Laisa » Ter Fev 26, 2019 17:02
por Laisa » Ter Fev 26, 2019 17:02
Dado a função
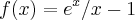
Faça a derivada da primeira e a derivada da segunda.
-
Laisa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Fev 19, 2019 21:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por DanielFerreira » Qui Set 05, 2019 23:28
por DanielFerreira » Qui Set 05, 2019 23:28
Considere
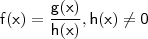
. De acordo com a regra do quociente,
![\boxed{\mathsf{f'(x) = \dfrac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}}} \boxed{\mathsf{f'(x) = \dfrac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}}}](/latexrender/pictures/d0700ee76243a8a4d818be6b215d8f84.png)
Dito isto, temos que:
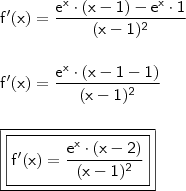
Para determinar a derivada segunda, aplique novamente a regra do quociente...
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada primeira e segunda
por luiz3107 » Ter Ago 17, 2010 16:39
- 2 Respostas
- 2930 Exibições
- Última mensagem por luiz3107

Ter Ago 17, 2010 17:54
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de primeira e segunda ordem
por Nina » Qui Nov 05, 2009 20:52
- 1 Respostas
- 4117 Exibições
- Última mensagem por marciommuniz

Sex Nov 06, 2009 13:02
Cálculo: Limites, Derivadas e Integrais
-
- Derivada primeira
por LAZAROTTI » Dom Jun 24, 2012 17:33
- 1 Respostas
- 1742 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 18:38
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Primeira]
por LAZAROTTI » Ter Dez 11, 2012 21:52
- 1 Respostas
- 1825 Exibições
- Última mensagem por e8group

Ter Dez 11, 2012 22:29
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de primeira ordem.
por Sobreira » Sex Mar 08, 2013 01:14
- 1 Respostas
- 1857 Exibições
- Última mensagem por Russman

Sex Mar 08, 2013 04:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
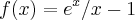

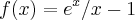

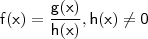 . De acordo com a regra do quociente,
. De acordo com a regra do quociente,![\boxed{\mathsf{f'(x) = \dfrac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}}} \boxed{\mathsf{f'(x) = \dfrac{g'(x) \cdot h(x) - g(x) \cdot h'(x)}{[h(x)]^2}}}](/latexrender/pictures/d0700ee76243a8a4d818be6b215d8f84.png)