Então, estou tendo muita dificuldade de achar limites de integração depois de feita uma mudança de variáveis, porque nem sempre sei qual o gráfico que a mudança gera nem sei como se deveria calcular algebricamente. Vejo o pessoal fazendo certos calculos pra achar, mas n entendo qual a lógica, se alguém pudesse explicar seria ótimo. Um exemplo em que não sei como calcular:
1. Use coordenadas polares e calcule as seguintes integrais duplas:
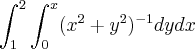
Os exemplos mais "triviais" são okay, mas esses exemplos q precisa de algum calculo ou coisa do tipo n entendo como deve ser feito. Pensei em substituir x^2+y^2 por r^2 mas sinceramente n sei oq fzr dps dai


![\\
x=rcos(\theta)\\
y=rsen(\theta)\\
\sqrt[]{x^2+y^2}=r\\
dxdy=rd\theta dr \\
x=rcos(\theta)\\
y=rsen(\theta)\\
\sqrt[]{x^2+y^2}=r\\
dxdy=rd\theta dr](/latexrender/pictures/81b37ed59b866c0c1485b638881b6ebf.png)


![\\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\int_{0}^{\frac{\pi}{4}}\frac{1}{r^2}rd\theta dr\\
\\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\int_{0}^{\frac{\pi}{4}}\frac{1}{r}d\theta dr\\
\\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\left\frac{\theta}{r}\right|_{0}^{\frac{\pi}{4}} dr
\\
\frac{\pi}{4}\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\frac{1}{r} dr\\
\\
\frac{\pi}{4}\left(ln\left|2\sqrt[]{2} \right|-ln\left|\sqrt[]{2} \\
\\\right| \right)\\
\\
\frac{\pi}{4}\left(ln\left(2\sqrt[]{2} \right)-ln\left(\sqrt[]{2} \\
\\\right) \right)\\
\\
\frac{\pi}{4}ln(2) \\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\int_{0}^{\frac{\pi}{4}}\frac{1}{r^2}rd\theta dr\\
\\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\int_{0}^{\frac{\pi}{4}}\frac{1}{r}d\theta dr\\
\\
\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\left\frac{\theta}{r}\right|_{0}^{\frac{\pi}{4}} dr
\\
\frac{\pi}{4}\int_{\sqrt[]{2}}^{2\sqrt[]{2}}\frac{1}{r} dr\\
\\
\frac{\pi}{4}\left(ln\left|2\sqrt[]{2} \right|-ln\left|\sqrt[]{2} \\
\\\right| \right)\\
\\
\frac{\pi}{4}\left(ln\left(2\sqrt[]{2} \right)-ln\left(\sqrt[]{2} \\
\\\right) \right)\\
\\
\frac{\pi}{4}ln(2)](/latexrender/pictures/a039b197e2029c7f0d74dbd95195d70a.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)