estou estudando um artigo sobre a influência da resistência do ar em uma trajetória de lançamento oblíquo.
Acontece que não compreendi como o autor do artigo chegou a integral de uma função.

Ele integrou a função (5) que dá a aceleração da partícula:
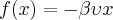
Dados:

Onde b é uma constante da Força de Resistência do Ar,
e m é a massa da partícula.

Sendo F = m * a, ao dividir por m (massa) vou ter apenas a aceleração. No caso, a função (5).
Sabendo que:
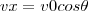
Então a função que foi integrada, me parece que foi:

E a função obtida foi:
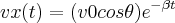
Gostaria de compreender como ele chegou a esse resultado através de integral.
Compreendo que a integral da equação da aceleração em função do tempo será a equação da velocidade em função do tempo.
Não compreendi as substituições que foram utilizadas.
Obrigado.


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.