 por matmatco » Qui Jun 29, 2017 08:28
por matmatco » Qui Jun 29, 2017 08:28
O exercício é:
Prove que se
![f,g:\left[a,b \right]\rightarrow R f,g:\left[a,b \right]\rightarrow R](/latexrender/pictures/8153e03ebe0f1b487e7d2c21861fd4df.png)
são integráveis então são também integráveis as funções
![\varphi,\psi:\left[a,b \right]\rightarrow R \varphi,\psi:\left[a,b \right]\rightarrow R](/latexrender/pictures/53cba75fa2b18469d374358495d70aa1.png)
, definidas por

e

. Conclua daí que são integráveis as funções
![{f}_{+},{f}_{-}:\left[a,b \right]\rightarrow R {f}_{+},{f}_{-}:\left[a,b \right]\rightarrow R](/latexrender/pictures/557b97311c9350c41a8a236105766406.png)
dadas por
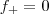
se
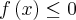
,

se

;
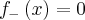
se
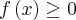
e
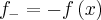
se
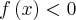
(supondo f integrável).
minha dúvida é como escrever que a oscilação da

é

que a oscilação de

.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por adauto martins » Ter Jul 11, 2017 15:12
por adauto martins » Ter Jul 11, 2017 15:12
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por matmatco » Qua Jul 12, 2017 17:08
por matmatco » Qua Jul 12, 2017 17:08
Olá Adauto, tudo bem?
Não entendi o que vc quis dizer ficou muito confuso, mas consegui resolver a questão. Segue a solução caso queira saber.
Sabemos que
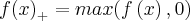
e
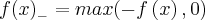
então

, logo
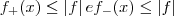

e
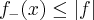
, integrando nós temos
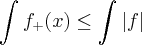
sendo f integrável implica
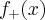
também é integrável.( análogo para
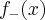
.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por adauto martins » Qui Jul 13, 2017 13:06
por adauto martins » Qui Jul 13, 2017 13:06
a sua duvida era qdo as oscilaçao de
![f(x),w(f(x),[a,b])...{f}_{+},w({f}_{+},[a,b)} f(x),w(f(x),[a,b])...{f}_{+},w({f}_{+},[a,b)}](/latexrender/pictures/917b9b4b0b2419ccc547619216fc946f.png)
,pela definiçao dada pelo problema,conclui o q. fiz...no ponto

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Análise Real/Sequencia
por Raphaelphtp » Seg Jan 16, 2017 15:24
- 1 Respostas
- 2408 Exibições
- Última mensagem por adauto martins

Ter Jan 17, 2017 10:33
Cálculo: Limites, Derivadas e Integrais
-
- analise real como proceder
por caciano-death » Sex Ago 25, 2017 17:56
- 2 Respostas
- 2122 Exibições
- Última mensagem por adauto martins

Qua Ago 30, 2017 11:36
Cálculo: Limites, Derivadas e Integrais
-
- ANÁLISE REAL: FUNÇÃO LIMITADA
por renataribeiro2017 » Sex Set 08, 2017 12:28
- 2 Respostas
- 6020 Exibições
- Última mensagem por adauto martins

Ter Mai 01, 2018 21:16
Cálculo: Limites, Derivadas e Integrais
-
- Análise Real : Números Reais (desigualdade de Cauchy-Schwar
por JorgeVidal » Dom Fev 22, 2015 18:00
- 1 Respostas
- 3628 Exibições
- Última mensagem por adauto martins

Qua Fev 25, 2015 20:49
Teoria dos Números
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3262 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f,g:\left[a,b \right]\rightarrow R f,g:\left[a,b \right]\rightarrow R](/latexrender/pictures/8153e03ebe0f1b487e7d2c21861fd4df.png) são integráveis então são também integráveis as funções
são integráveis então são também integráveis as funções ![\varphi,\psi:\left[a,b \right]\rightarrow R \varphi,\psi:\left[a,b \right]\rightarrow R](/latexrender/pictures/53cba75fa2b18469d374358495d70aa1.png) , definidas por
, definidas por  e
e  . Conclua daí que são integráveis as funções
. Conclua daí que são integráveis as funções ![{f}_{+},{f}_{-}:\left[a,b \right]\rightarrow R {f}_{+},{f}_{-}:\left[a,b \right]\rightarrow R](/latexrender/pictures/557b97311c9350c41a8a236105766406.png) dadas por
dadas por 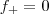 se
se 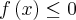 ,
,  se
se  ;
; 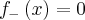 se
se 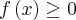 e
e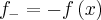 se
se 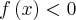 (supondo f integrável).
(supondo f integrável). é
é  que a oscilação de
que a oscilação de  .
.

 ,logo:
,logo: 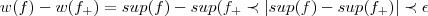 ,como
,como 

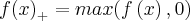 e
e 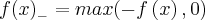 então
então  , logo
, logo 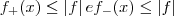
 e
e 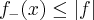 , integrando nós temos
, integrando nós temos 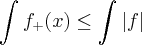 sendo f integrável implica
sendo f integrável implica 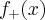 também é integrável.( análogo para
também é integrável.( análogo para 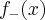 .
.![f(x),w(f(x),[a,b])...{f}_{+},w({f}_{+},[a,b)} f(x),w(f(x),[a,b])...{f}_{+},w({f}_{+},[a,b)}](/latexrender/pictures/917b9b4b0b2419ccc547619216fc946f.png) ,pela definiçao dada pelo problema,conclui o q. fiz...no ponto
,pela definiçao dada pelo problema,conclui o q. fiz...no ponto 
