 por grey » Qua Fev 15, 2017 19:08
por grey » Qua Fev 15, 2017 19:08
Como é possível determinar a aceleração, a velocidade e o espaço nos 2 primeiros segundos de movimentos na seguinte equação: a(t) = t² + 3?
Estou com dificuldades em começar a integrar a equação da aceleração para achar a velocidade, para então posteriormente integrar a velocidade e achar o espaço.
-
grey
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Fev 15, 2017 18:39
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qui Fev 16, 2017 17:12
por adauto martins » Qui Fev 16, 2017 17:12
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral de uma Aceleração
por Atirador » Sáb Nov 18, 2017 18:36
- 0 Respostas
- 5325 Exibições
- Última mensagem por Atirador

Sáb Nov 18, 2017 18:36
Cálculo: Limites, Derivadas e Integrais
-
- Integrar exp
por LBT » Qui Jan 13, 2011 09:05
- 4 Respostas
- 2251 Exibições
- Última mensagem por LBT

Sex Jan 14, 2011 07:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Velocidade e Aceleração
por Fabio Cabral » Ter Jun 14, 2011 14:49
- 1 Respostas
- 4450 Exibições
- Última mensagem por carlosalesouza

Ter Jun 14, 2011 15:40
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Problema com aceleração
por MrJuniorFerr » Sáb Nov 10, 2012 20:19
- 4 Respostas
- 3292 Exibições
- Última mensagem por young_jedi

Sáb Nov 10, 2012 21:37
Cálculo: Limites, Derivadas e Integrais
-
- Derivada, velocidade e aceleração
por Janoca » Ter Jun 24, 2014 17:08
- 1 Respostas
- 1739 Exibições
- Última mensagem por Janoca

Ter Jun 24, 2014 18:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![v(2)-v(0)=({t}^{3}/3)[0,2]+3.t[0,2] v(2)-v(0)=({t}^{3}/3)[0,2]+3.t[0,2]](/latexrender/pictures/f89f695e33fcb2b45ed651c698d34d44.png) ,bom nao foi dito se o movel,ou particula partiu do repouso,onde
,bom nao foi dito se o movel,ou particula partiu do repouso,onde 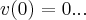
![v(t)=({t}^{3}/3)+3t...v(t)=ds/dt\Rightarrow ds=({t}^{3}/3)dt+3tdt\Rightarrow \int_{0}^{2}ds=\int_{0}^{2}({t}^{3}/3)dt+3.\int_{0}^{2}tdt\Rightarrow s(2)-s(0)=({t}^{4}/12)[0,2]+3.({t}^{2}/2)[0,2]... v(t)=({t}^{3}/3)+3t...v(t)=ds/dt\Rightarrow ds=({t}^{3}/3)dt+3tdt\Rightarrow \int_{0}^{2}ds=\int_{0}^{2}({t}^{3}/3)dt+3.\int_{0}^{2}tdt\Rightarrow s(2)-s(0)=({t}^{4}/12)[0,2]+3.({t}^{2}/2)[0,2]...](/latexrender/pictures/c4990318f0f372f009d734f3c4a7e69f.png)

