Boa noite maiquel.
Não lhe vou resolver a integral porque sinceramente não sei como a resolver. Mas, segundo uma calculadora TI-Nspire CX CAS, o resultado é como se segue:

- Int. dupla de volume.jpg (15.79 KiB) Exibido 6200 vezes
No WolframAlpha, se você digitar como mostra a imagem vai obter exactamente o mesmo valor.
Veja que, quando se inclina o cilindro de modo a provocar um desnivelamento de
1cm sobre qualquer ponto do rebordo do fundo do mesmo em relação ao plano, se vai gerar um "tronco de cilindro reto". Como o conteúdo do cilindro é liquido se o mesmo estiver cheio irá transbordar, e o volume desse transbordo, será exatamente o volume do "tronco de cilindro reto", que nesse caso tem as dimensões de
1cm de inclinação em relação ao ponto de apoio no plano e
0,5 m de raio. Repare que o
"Volume 3"=
Volume 2 que por sua vez é igual ao
Volume 1 que foi o volume de água transbordada.
Veja o vídeo abaixo que foi de onde tirei as figuras para ilustrar mais especificamente o seu caso.
https://www.youtube.com/watch?v=q5catnb4QMwConsiderando a fórmula do "Tronco de cilindro reto" dada na imagem acima, neste caso em concreto temos que:
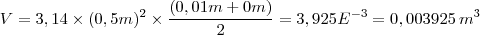
Como
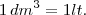
reduzimos os metros cúbicos a litros, e deste modo ficamos com

esta foi a quantidade de água que transbordou ao se inclinar o cilindro em 1cm.
Dado que o volume do cilindro é dado por:
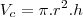
temos:

Portanto quando o cilindro está
1 cm desnivelado o volume será de:
Volume total - transbordo
Creio que seja esse o valor.
Agora qual o valor da integral na resolução do problema, francamente não sei.
Se você ou algum outro usuário souberem e chegarem na resolução por favor postem ela aqui.
![v=\int_{-0,5}^{0,5} \int_{-\sqrt[]{0,5²x²}}^{\sqrt[]{0,5²x²}} -y +0,5 dy dx v=\int_{-0,5}^{0,5} \int_{-\sqrt[]{0,5²x²}}^{\sqrt[]{0,5²x²}} -y +0,5 dy dx](/latexrender/pictures/d5f0cc03842cc203eff7010dd5de502d.png)


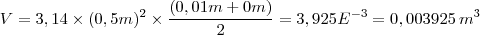
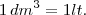 reduzimos os metros cúbicos a litros, e deste modo ficamos com
reduzimos os metros cúbicos a litros, e deste modo ficamos com 
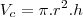 temos:
temos:


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)