


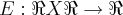 ,tal que
,tal que  ...
... é topologico,mas nao metrico,pois:
é topologico,mas nao metrico,pois: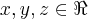 ,nem sempre podemos ter:
,nem sempre podemos ter:

 é espaço topológico mas não é espaço métrico, pois aquela função d(x, y) não caracteriza uma métrica. Agora a minha duvida tá em saber se essa mesma função d( x, y) é que fornece os abertos da topologia de
é espaço topológico mas não é espaço métrico, pois aquela função d(x, y) não caracteriza uma métrica. Agora a minha duvida tá em saber se essa mesma função d( x, y) é que fornece os abertos da topologia de  ?
?
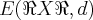 é espaço metrico dependendo da metrica
é espaço metrico dependendo da metrica  ...
...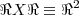 ,tais como:
,tais como:![d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc... d(x,y)=\left|x-y \right|...d={x}^{2}+{y}^{2}...d=\left|{x}^{2}-{y}^{2} \right|...d=\sqrt[]{{x}^{2}+{y}^{2}}(mostre-as!)..etc...](/latexrender/pictures/25f8be7cac72f2847dc43ade7645d25b.png) ...
...

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)