 por ramoncampos » Ter Nov 01, 2016 21:20
por ramoncampos » Ter Nov 01, 2016 21:20
Boa noite Pessoal! Tudo bem com vocês?
Eu tenho um exercício que fiquei em dúvida, primeiramente, e aguardarei uma ajuda para a resolução. É o seguinte:
Prove que f(x) = x³ é contínua em p = 2
f(2) = 2³ = 8
Bom, por definição, para todo E > 0 , existe d > 0 tal que |x-2| < d => |f(x)-f(2)| < E .
Desenvolvendo |f(x)-f(2)| < E => |x^3-8| < E => |x^3-2^3| < E => |(x-2)*(x^2+2x+4)| < E => |x-2|*|x^2+2x+4| < E
Daí em diante não sei o que exatamente fazer. Por um livro, descobri que tenho que limitar |x^2+2x+4| porém não sei como fazer isto.
Obrigado a Todos! Bons Estudos!

Obs: E: epsilon e d: delta
-
ramoncampos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 28, 2015 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Qui Nov 03, 2016 12:04
por adauto martins » Qui Nov 03, 2016 12:04
a questao é:
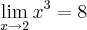
...no formalismo:
dado

,tal q.

...
temos q.

é raiz do polinomio
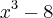
,logo
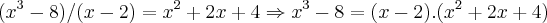
...

,nao tem raizes reais,pois
,entao nao temos como reduzir o seu grau p/valores reais...logo:
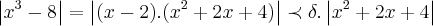
...
temos por hipotese q.:
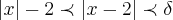
,desiqualdade triangular

...portanto:
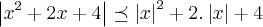
,aqui tbem a des.triangular...
portanto:

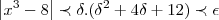
...pela def. p/um
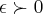
dado existe pelo um
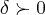
,o qual procuramos o menor,ou seja
![\delta=min[{\delta}_{1},{\delta}_{2},...] \delta=min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/f2a9587965729748f48d2cae0c7f11ba.png)
...geralmente,e o mais correto é tomarmos
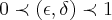
...logo se tomarmos um num.
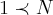
,podemos ter:

...o correto mesmo era resolver a inequaçao

e encontrar o menor
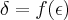
,mas o exposto acima esta tbem correto...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por ramoncampos » Qui Nov 03, 2016 17:22
por ramoncampos » Qui Nov 03, 2016 17:22
Muito obrigado! Mas o que significa esse min {d1,d2,...} ?
Obrigado!

-
ramoncampos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 28, 2015 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Sex Nov 04, 2016 11:11
por adauto martins » Sex Nov 04, 2016 11:11
em cada
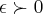
dado,procuramos nos infinitos
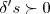
o menor

possivel...ai escreve-se dessa forma
![\delta=min[{\delta}_{1},{\delta}_{2}...] \delta=min[{\delta}_{1},{\delta}_{2}...]](/latexrender/pictures/00a6880ee6c56acc6f4110639dfba122.png)
,min[...] toma a conotaçao de menor dos deltas possiveis...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por ramoncampos » Sex Nov 04, 2016 12:39
por ramoncampos » Sex Nov 04, 2016 12:39
Entendi! Muito Obrigado amigo!

-
ramoncampos
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mar 28, 2015 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites pela definição formal
por joaofonseca » Ter Out 11, 2011 09:38
- 1 Respostas
- 2751 Exibições
- Última mensagem por joaofonseca

Qua Out 12, 2011 19:29
Cálculo: Limites, Derivadas e Integrais
-
- [limites] Propriedades ou definição formal?
por jvabatista » Qua Jun 06, 2012 11:43
- 3 Respostas
- 3426 Exibições
- Última mensagem por adauto martins

Ter Out 14, 2014 20:05
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com a definição formal de limites
por Gustavooguto » Seg Out 13, 2014 23:49
- 1 Respostas
- 2367 Exibições
- Última mensagem por adauto martins

Ter Out 14, 2014 11:19
Funções
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6102 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- Limites pela definição
por Fred Pellegrini » Sex Out 28, 2016 18:21
- 1 Respostas
- 4663 Exibições
- Última mensagem por adauto martins

Seg Out 31, 2016 10:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



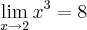 ...no formalismo:
...no formalismo: ,tal q.
,tal q.  ...
... é raiz do polinomio
é raiz do polinomio 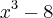 ,logo
,logo 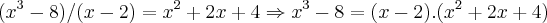 ...
... ,nao tem raizes reais,pois
,nao tem raizes reais,pois 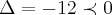 ,entao nao temos como reduzir o seu grau p/valores reais...logo:
,entao nao temos como reduzir o seu grau p/valores reais...logo: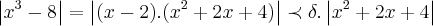 ...
...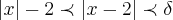 ,desiqualdade triangular
,desiqualdade triangular ...portanto:
...portanto: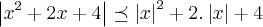 ,aqui tbem a des.triangular...
,aqui tbem a des.triangular...
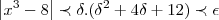 ...pela def. p/um
...pela def. p/um 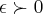 dado existe pelo um
dado existe pelo um 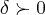 ,o qual procuramos o menor,ou seja
,o qual procuramos o menor,ou seja ![\delta=min[{\delta}_{1},{\delta}_{2},...] \delta=min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/f2a9587965729748f48d2cae0c7f11ba.png) ...geralmente,e o mais correto é tomarmos
...geralmente,e o mais correto é tomarmos 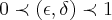 ...logo se tomarmos um num.
...logo se tomarmos um num.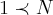 ,podemos ter:
,podemos ter: ...o correto mesmo era resolver a inequaçao
...o correto mesmo era resolver a inequaçao  e encontrar o menor
e encontrar o menor 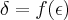 ,mas o exposto acima esta tbem correto...
,mas o exposto acima esta tbem correto...
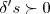 o menor
o menor  possivel...ai escreve-se dessa forma
possivel...ai escreve-se dessa forma ![\delta=min[{\delta}_{1},{\delta}_{2}...] \delta=min[{\delta}_{1},{\delta}_{2}...]](/latexrender/pictures/00a6880ee6c56acc6f4110639dfba122.png) ,min[...] toma a conotaçao de menor dos deltas possiveis...
,min[...] toma a conotaçao de menor dos deltas possiveis...




