Determine os pontos de máximo e mínimo locais da função
 , dizendo quais destes pontos são máximos ou mínimos globais.
, dizendo quais destes pontos são máximos ou mínimos globais.O que eu fiz para encontrar os pontos de mínimo locais:
1º - Derivei a função:

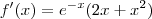
2º - Igualei a função a zero para encontrar os pontos críticos:
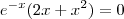
Como
 é sempre positivo, a função só poderá ser zero quando
é sempre positivo, a função só poderá ser zero quando 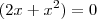 . Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.
. Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.3º - Calculei a f'(x) para -3 , -1 e 1 para saber se a função é crescente ou decrescente antes e depois dos pontos críticos.
 (positivo)
(positivo)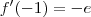 (negativo)
(negativo)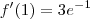 (positivo)
(positivo)4º - Determinei os pontos de mínimo e máximo locais:
Como a função é crescente antes de -2 e decrescente após o -2, logo ele é um ponto de máximo local.
E como a função é decrescente antes do 0 e crescente após 0 , ele é um ponto de mínimo local.
A partir de agora eu não sei o que devo fazer para encontrar os pontos de máximo e mínimo globais, caso existam.
Obs: O gabarito da questão informa que a função não possui máximo global e que o ponto 0 é mínimo global.



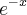 pela regra
pela regra 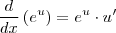 obtemos
obtemos  .
.
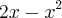 são 0 e 2.
são 0 e 2.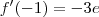 (negativo, portanto decrescente)
(negativo, portanto decrescente) (positivo, portanto crescente)
(positivo, portanto crescente) (negativo, portanto decrescente)
(negativo, portanto decrescente) da derivada da função original que usamos para encontrar os pontos críticos é uma parábola. Nos intervalos onde esta parábola tem imagem negativa, a função original é decrescente. No intervalo onde esta parábola tem imagem positiva, a função original é crescente. O
da derivada da função original que usamos para encontrar os pontos críticos é uma parábola. Nos intervalos onde esta parábola tem imagem negativa, a função original é decrescente. No intervalo onde esta parábola tem imagem positiva, a função original é crescente. O  nem
nem  , que é maior que 2. Portanto, 2 é máximo local.
, que é maior que 2. Portanto, 2 é máximo local.

 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.