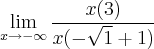por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
Olá, estou com dúvida na seguinte questão.
1 )

(Essa é a letra B da questão 82 do Livro do Iezzi Vol.8)
Quando tendo resolver a questão resulta nisto
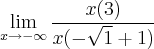
Veja que o denominar iria resultar em zero, e além disto, no solucionário do livro diz que a resposta é


<-- Forma como está no solucionário
Agradeço a atenção;
- Anexos
-
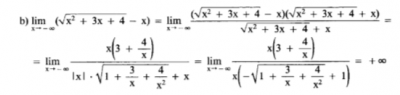
- Em anexo a quem não conseguir ver
-
Jacques
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jul 12, 2016 21:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por vitor_jo » Qua Jul 13, 2016 06:30
por vitor_jo » Qua Jul 13, 2016 06:30
Vê só, estou meio enrolado aqui, mas acho que isso pode ajudar.
Partindo dessa última expressão, antes do infinito
Cortando x em cima e embaixo tem-se
lim x> - infinito (3+4/x) / (-(1+3/x+4/x²)^(1/2)+1)
Ok, nada novo.
Tomando 3 +4/x= u, limx-> - infinito, u--> 3 (pela esquerda)
Se 3+4/x=4, 3/x +4x² =u/x
Agora volta isso lá em cima,
lim u-> 3 (pela esquerda) u/[(-(1+u/x)^(1/2) +1)] *
Como 3 +4/x= u, então x= 4/(u-3), voltando na equação acima
lim u->3 (esqu) u/-[1+(u/4/u-3)^(1/2)+1] = u/[-(1+(u²-3u)/4)^(1/2) +1]
Jogando o limite, 3(esq)/[-(1+0/4)^(1/2)+1]
Admiti x->3(esq) para ser rigoroso. A ideia é que ficaria
3(esq)/[-(1-0.0000..1)^(1/2) +1] ->>> 3(esq)/um número positivo mas que tende a zero pela direta.
Assim dá + infinito.
-
vitor_jo
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qua Jan 14, 2015 05:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por vitor_jo » Qua Jul 13, 2016 06:31
por vitor_jo » Qua Jul 13, 2016 06:31
(perdão pela escrita em extenso, ainda não dominei o latex)
-
vitor_jo
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qua Jan 14, 2015 05:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por Jacques » Qua Jul 13, 2016 13:50
por Jacques » Qua Jul 13, 2016 13:50
Agradeço pela resposta, eu consegui entender a escrita sem problemas. Quando questionei ao meu professor ele também citou que esse denominador não daria 0 e sim um numero bem pequeno, mas ele não fez todo esse processo.
Grato por sua atenção
-
Jacques
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jul 12, 2016 21:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por vitor_jo » Qua Jul 13, 2016 16:51
por vitor_jo » Qua Jul 13, 2016 16:51
Sim, eu pensei em não desenvolver tudo isso, mas não estava convencido que dava p/ mais infinito a coisa, daí fui manipular. :P
Abraço.
-
vitor_jo
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qua Jan 14, 2015 05:36
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida superficial - limites no infinito
por phfrito » Qui Mai 08, 2014 19:26
- 4 Respostas
- 2880 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 14:54
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4771 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3520 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Limites no "infinito " prova a existência ......
por e8group » Dom Jun 17, 2012 14:37
- 2 Respostas
- 2748 Exibições
- Última mensagem por e8group

Ter Jun 19, 2012 11:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] limites no infinito
por lucasdemirand » Qui Jul 11, 2013 15:10
- 1 Respostas
- 1458 Exibições
- Última mensagem por e8group

Qui Jul 11, 2013 15:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 (Essa é a letra B da questão 82 do Livro do Iezzi Vol.8)
(Essa é a letra B da questão 82 do Livro do Iezzi Vol.8)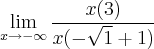


 (Essa é a letra B da questão 82 do Livro do Iezzi Vol.8)
(Essa é a letra B da questão 82 do Livro do Iezzi Vol.8)