 ,onde
,onde  é um espaço vetorial sobre um corpo
é um espaço vetorial sobre um corpo 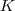 é dado por:
é dado por: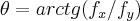 ,onde
,onde  sao derivadas parcias e
sao derivadas parcias e  um angulo do circulo trigonometrico.
um angulo do circulo trigonometrico.
 ,onde
,onde  é um espaço vetorial sobre um corpo
é um espaço vetorial sobre um corpo 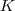 é dado por:
é dado por: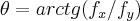 ,onde
,onde  sao derivadas parcias e
sao derivadas parcias e  um angulo do circulo trigonometrico.
um angulo do circulo trigonometrico.


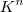 valorada em K , onde K pode ser tanto os reais quanto os complexos .. Não pode ser um corpo arbitrário , se não cai no problema de não ter ponto acumulação .. Pensa num negocio esquisito como
valorada em K , onde K pode ser tanto os reais quanto os complexos .. Não pode ser um corpo arbitrário , se não cai no problema de não ter ponto acumulação .. Pensa num negocio esquisito como  etc .. ) .. Para falar de ângulo é preciso ter produto interno então qm sabe há uma generalização para Hilbert spaces .. para aplicações entre espaços de Banach (podendo ser não completo contitua fazendo sentido ) a noção de derivada num ponto faz sentido , mas agora será uma transformação afim que melhror aproxima a função perto do ponto ... De forma análoga , a noção de derivada parcial faz sentido para função entre espaços normados só que agora o espaço precisa ser decomposto como soma direta para introduzir tal definição ..
etc .. ) .. Para falar de ângulo é preciso ter produto interno então qm sabe há uma generalização para Hilbert spaces .. para aplicações entre espaços de Banach (podendo ser não completo contitua fazendo sentido ) a noção de derivada num ponto faz sentido , mas agora será uma transformação afim que melhror aproxima a função perto do ponto ... De forma análoga , a noção de derivada parcial faz sentido para função entre espaços normados só que agora o espaço precisa ser decomposto como soma direta para introduzir tal definição ..

 .. Se
.. Se 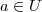 for ponto de acumulação de
for ponto de acumulação de 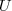 e as derivadas parciais de f (que vou denotar-lás por
e as derivadas parciais de f (que vou denotar-lás por  , como uma notação sugestiva para a generalização , para espaços mais gerais até de dim infinita ) .. Define-se então o vetor
, como uma notação sugestiva para a generalização , para espaços mais gerais até de dim infinita ) .. Define-se então o vetor 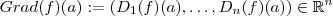 .. Agora , se U for aberto , todos os ponto dele serão de acumulação [Bom exercício ! Se não fez , faça ] , e se todas derivadas parciais de f existirem em todos pontos de U , a correspondência
.. Agora , se U for aberto , todos os ponto dele serão de acumulação [Bom exercício ! Se não fez , faça ] , e se todas derivadas parciais de f existirem em todos pontos de U , a correspondência  define uma função (vetorial )
define uma função (vetorial )  .
.
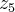 ,q. nao é corpo,é grupo...
,q. nao é corpo,é grupo... (prove isso!se vc entender ne)...nao direi nada sobre espaços de banach,hilbert q. ne,se vc nao sabe o q. é um espaço vetorial?entao...
(prove isso!se vc entender ne)...nao direi nada sobre espaços de banach,hilbert q. ne,se vc nao sabe o q. é um espaço vetorial?entao... ,somente pra efeito de sintese,de ilustraçao,depois ,uma outra hora faço p/(
,somente pra efeito de sintese,de ilustraçao,depois ,uma outra hora faço p/( )...
)...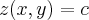 ...qquer ponto dessa curva é dado pelo vetor posiçao(x,y),cujo unitario pode ser dado por
...qquer ponto dessa curva é dado pelo vetor posiçao(x,y),cujo unitario pode ser dado por 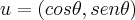 ,logo
,logo  ,onde
,onde  é o vetor gradiente...logo,
é o vetor gradiente...logo,

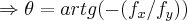 ,como a funçao arctg é uma funçao impar(prove isso!se entender)
,como a funçao arctg é uma funçao impar(prove isso!se entender)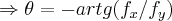 ...cqd...
...cqd...
adauto martins escreveu:blabla,blabla santiago...
estude matematica mesmo e pare de copiar do wiki,ou livros q. vc nao entende nada...
primeiramente um espaço vetorial e definido sobre um corpo...vc cita {z}_{5},q. nao é corpo,é grupo...
 é corpo sim ! Na verdade
é corpo sim ! Na verdade 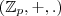 é corpo se e seomente
é corpo se e seomente  é primo !
é primo ! 

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

