[Taxas relacionadas] Derivadas

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Taxas relacionadas] Derivadas

Regras do fórum
Responder

[Taxas relacionadas] Derivadas

Mensagempor rzarour » Seg Fev 29, 2016 15:05

Prezados(as), resolvi uma questão de taxas relacionadas sem, no entanto, saber a resposta através de gabarito ou outro meio. Segue enunciado abaixo:

Um homem numa doca atira uma corda para um homem num barco; este amarra a corda ao barco. O homem da doca puxa então o barco em sua direção. Se as mãos do homem estiverem 8 pés acima da água e se ele puxar a corda à razão de 2 pés/seg, determinar a velocidade a que o barco se aproxima da base da doca quando ainda existir 10 pés de corda sobrando para serem puxados.

O que chamei de 'solução' iniciou-se com um triângulo retângulo formado pela corda jogada da doca para o barco (lado C do triângulo), a distância entre as mãos do homem da doca e a água (lado A do triângulo) e, através de Pitágoras, a distância entre o barco e a doca (lado B):

B = \sqrt[]{{C}^{2} - {A}^{2}} = 6 pés

Considerando ainda o Teorema, reescrevi a relação e em seguida derivei cada membro:

{C}^{2} = {A}^{2} + {B}^{2}

\frac{d({C}^{2})}{dt} = \frac{d({A}^{2})}{dt} + \frac{d({B}^{2})}{dt}

2C\frac{d(C)}{dt} = 2A\frac{d(A)}{dt} + 2B\frac{d(B)}{dt}

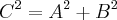
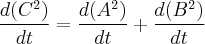
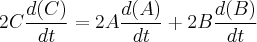
Substituindo pelos dados fornecidos no enunciado cheguei ao seguinte resultado:

20 * 2 = 16 * 0 + 12\frac{d(B)}{dt}

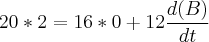
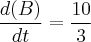\frac{d(B)}{dt} = \frac{10}{3} pés/seg

Seria esta a resposta correta ou cometi erro(s) durante a interpretação e resolução do problema?

Grato!
rzarour
Novo Usuário
Novo Usuário
 
Mensagens: 4
Registrado em: Seg Fev 29, 2016 02:05
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Técnico em Eletrotécnica
Andamento: formado
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum