 por eulercx » Sáb Nov 14, 2015 10:27
por eulercx » Sáb Nov 14, 2015 10:27
-
eulercx
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Nov 07, 2015 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Cleyson007 » Sáb Nov 14, 2015 20:08
por Cleyson007 » Sáb Nov 14, 2015 20:08
Olá amigo, boa noite!
Repare que a função f é racional (dada por um quociente P(x)/Q(x)). Logo, nos é conveniente aplicar a Regra do Quociente! Para isto, fazemos:
f'(x) = P'(x) * Q(x) - Q'(x) * P(x)] / [Q(x)]²
A partir daí consegue concluir sozinho?
Caso queira conhecer o meu trabalho enquanto professor de Matemática, acesse: viewtopic.php?f=151&t=13614
Bons estudos
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por eulercx » Sáb Nov 14, 2015 21:09
por eulercx » Sáb Nov 14, 2015 21:09
já fiz pela regra do quociente, mas o resultado não bate com o do livro
-
eulercx
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Nov 07, 2015 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Cleyson007 » Sáb Nov 14, 2015 22:09
por Cleyson007 » Sáb Nov 14, 2015 22:09
Sejam,
P(x) = -x² + 1
Q(x) = (x² + 1)²
Você está fazendo P'(x) = -2x e Q'(x) = 2(x² + 1)(2x)?
Por favor, poste o que você. Assim, eu comento onde está o seu erro (ou do gabarito).
Att,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Seg Nov 16, 2015 08:26
por Cleyson007 » Seg Nov 16, 2015 08:26
Eulercx, o erro está no numerador. O correto é:
}{(x^2+1)^4} f'(x)=\frac{(-2x)(x^2+1)^2-[2(x^2+1)(2x)](-x^2+1)}{(x^2+1)^4}](/latexrender/pictures/c6a5be8c32fccb2f20fbdc929c9d37b5.png)
Sou professor de Matemática e posso lhe ajudar bastante em seus estudos. Caso tenha interesse em conhecer o meu trabalho, acesse:
viewtopic.php?f=151&t=13614Abraço e bons estudos.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por eulercx » Seg Nov 16, 2015 09:35
por eulercx » Seg Nov 16, 2015 09:35
vlw

-
eulercx
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Nov 07, 2015 16:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- urgente como fazer a derivada
por jayne » Qua Ago 24, 2011 09:24
- 1 Respostas
- 2546 Exibições
- Última mensagem por MarceloFantini

Qua Ago 24, 2011 13:16
Cálculo: Limites, Derivadas e Integrais
-
- Como fazer uma função com essas condições
por Arthur_Bulcao » Sex Jun 29, 2012 03:42
- 4 Respostas
- 3152 Exibições
- Última mensagem por LuizAquino

Dom Jul 01, 2012 11:57
Funções
-
- Como achar a lógica dessa sentença
por oescolhido » Sex Fev 22, 2013 00:54
- 0 Respostas
- 2011 Exibições
- Última mensagem por oescolhido

Sex Fev 22, 2013 00:54
Lógica
-
- Exponencial de número complexo. Como saio dessa?
por andrina » Sex Nov 19, 2010 15:16
- 1 Respostas
- 2232 Exibições
- Última mensagem por luispereira

Sex Dez 24, 2010 13:24
Números Complexos
-
- como fazer?
por Amandatkm » Qui Mar 21, 2013 18:12
- 1 Respostas
- 2450 Exibições
- Última mensagem por timoteo

Qui Mar 21, 2013 20:56
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
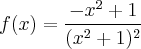






![\frac{-2x(x^2+1)^2+x^2-1*2(x^2+1)2x}{[(x^2+1)^2]^2}} =\frac{-2x(x^2+1)^2+x^2-1*4x(x^2+1)}{[(x^2+1)^2]^2} \frac{-2x(x^2+1)^2+x^2-1*2(x^2+1)2x}{[(x^2+1)^2]^2}} =\frac{-2x(x^2+1)^2+x^2-1*4x(x^2+1)}{[(x^2+1)^2]^2}](/latexrender/pictures/0d53c2af6dc26ea4f79ab3478a3b2027.png)
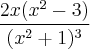

}{(x^2+1)^4} f'(x)=\frac{(-2x)(x^2+1)^2-[2(x^2+1)(2x)](-x^2+1)}{(x^2+1)^4}](/latexrender/pictures/c6a5be8c32fccb2f20fbdc929c9d37b5.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
