Seja a função f definida em [-3, 3] por g(x) =
![\sqrt[]{9 - {x}^{2}}](/latexrender/pictures/34b3c74e236b641a99a8d2c0b8898f1a.png "\sqrt[]{9 - {x}^{2}}")
. Verifique se f é contínua nesse intervalo.Resolução.
Determinando os limites laterais, temos:
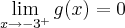
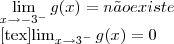
[/tex]
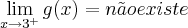
Como queremos saber se é contínua no intervalo [-3, 3], consideramos apenas o limite de -3 pela direita e o limite de 3 pela esquerda, como os valores são iguais, e f(-3) = f(3) = 0, a função é contínua nesse intervalo. ok
![\alpha(x)=\sqrt[]{x}](/latexrender/pictures/cc20a95db774eeb9b197e8e737100eb2.png "\alpha(x)=\sqrt[]{x}")
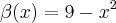
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)