Este exercício é do Cálculo B, da Flemming, de número 2.L, da página 242.
Devo esboçar a região de integração e calcular a integral iterada seguinte:
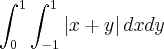
A solução dada pelo livro é
.O que fiz foi avaliar a região de integração e em seguida desenhar esta. Depois, avaliei a função módulo em questão e estabeleci os limites para os quais "o sinal troca".
Em seguida integrei para cada parte da função módulo e segui com a integral "de fora", mas obtive resposta 2. Tentei resolver pela HP 50g e obtive a resposta 1. A resposta está correta? Como devo resolver?
Segue imagem da minha resolução:
No Wolfram Alpha eu obtive a resposta correta. O que assegura que o livro está certo:
http://www.wolframalpha.com/share/clip? ... gjieqlrff9
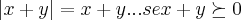
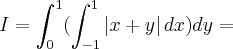
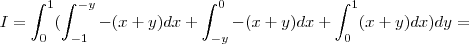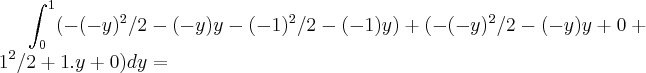
=![I=\int_{0}^{1}(-{x}^{2}-xy)[-1,-y]+(-{x}^{2}/2-xy)[-y,0])+({x}^{2}/2+xy[0,1])dy=](/latexrender/pictures/dcc353ff5145775fb28decc10071b6d3.png "I=\int_{0}^{1}(-{x}^{2}-xy)[-1,-y]+(-{x}^{2}/2-xy)[-y,0])+({x}^{2}/2+xy[0,1])dy=")
![\int_{0}^{1}(-{y}^{2}/2+{y}^{2}-1/2+y-{y}^{2}/2+{y}^{2}+1/2+y)dy=\int_{0}^{1}({y}^{2}+2y)dy={y}^{3}/3+{y}^{2})[0,1]=1/3+1=4/3](/latexrender/pictures/7d19738d5b805f851d8cbd18de736244.png "\int_{0}^{1}(-{y}^{2}/2+{y}^{2}-1/2+y-{y}^{2}/2+{y}^{2}+1/2+y)dy=\int_{0}^{1}({y}^{2}+2y)dy={y}^{3}/3+{y}^{2})[0,1]=1/3+1=4/3")
...
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.