Shirley,
Nesta regra de três, ocorre que se a eficiência de um é maior que a do outro, então, como consequência, ele fará o trabalho mais rapidamente. Como no enunciado foi dado que Y é 50% mais eficiente que X, lembrando que X = 1 pessoa e que 50% = 50/100 e que sendo mais eficiente que X, quer dizer que Y = 1 + 50/100, ou seja:

Então, sabendo-se que Y é 3/2 e X = 1, montamos a regra de três da seguinte forma:
Eficiência | Horas
1 | 12
3/2 ? | x ?
Temos aqui uma regra de três cujas proporções são inversamente proporcionais à outra. Ou seja:
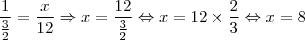
Logo, Y fará o mesmo trabalho em 8 horas.

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali




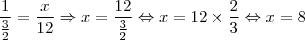



 .
.
 :
: