 por vitorvnm » Dom Jun 07, 2015 22:20
por vitorvnm » Dom Jun 07, 2015 22:20
Olá pessoal, alguém saberia me explicar esses dois exercícios de derivadas parciais ?
exercício 17 do stewart 7ª edição capítulo 14.3
17) F(x,t) =
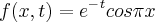
Pela regra da cadeia consegui fazer a derivada parcial em relação a x

ou seja, fiz uma regra da cadeia básica, derivando primeiro o cos e depois o pi x, mais não sei como fazer em relação a t
e do mesmo capítulo do stewart tem o exercício 35
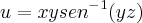
esse eu não consegui fazer nada, se pudessem explicar como se fosse pra uma criança de 11 anos eu agradeceria

-
vitorvnm
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 07, 2015 21:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por Cleyson007 » Seg Jun 08, 2015 10:16
por Cleyson007 » Seg Jun 08, 2015 10:16
Bom dia Vitor!
Seja muito bem-vindo ao fórum do Ajuda Matemática
 Questão 17
Questão 17:
Primeiramente, lembre-se que
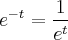
. Um outro detalhe importantíssimo é reparar que o (pi*x) é constante em relação à t. Logo, derivando parcialmente em relação a "t", tem-se:
 Questão 35
Questão 35: Você tem que derivar em relação à que?
Caso queira conhecer o nosso trabalho:
viewforum.php?f=151Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada Parcial de 1ª Ordem] - Derivada parcial num ponto
por Vitor2+ » Dom Jul 01, 2012 16:27
- 6 Respostas
- 4779 Exibições
- Última mensagem por e8group

Seg Jul 02, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- derivada parcial
por jmario » Dom Abr 18, 2010 11:41
- 0 Respostas
- 1795 Exibições
- Última mensagem por jmario

Dom Abr 18, 2010 11:41
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Parcial
por Silva339 » Seg Mar 25, 2013 19:06
- 1 Respostas
- 1932 Exibições
- Última mensagem por DanielFerreira

Sex Mar 29, 2013 02:28
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Parcial]
por Russman » Qui Mar 28, 2013 22:04
- 1 Respostas
- 1687 Exibições
- Última mensagem por Russman

Sex Mar 29, 2013 13:00
Cálculo: Limites, Derivadas e Integrais
-
- Derivada parcial
por guilherme5088 » Seg Mar 23, 2020 17:55
- 1 Respostas
- 4354 Exibições
- Última mensagem por guilherme5088

Seg Mar 23, 2020 17:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
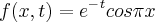
 ou seja, fiz uma regra da cadeia básica, derivando primeiro o cos e depois o pi x, mais não sei como fazer em relação a t
ou seja, fiz uma regra da cadeia básica, derivando primeiro o cos e depois o pi x, mais não sei como fazer em relação a t 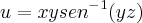 esse eu não consegui fazer nada, se pudessem explicar como se fosse pra uma criança de 11 anos eu agradeceria
esse eu não consegui fazer nada, se pudessem explicar como se fosse pra uma criança de 11 anos eu agradeceria 



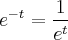 . Um outro detalhe importantíssimo é reparar que o (pi*x) é constante em relação à t. Logo, derivando parcialmente em relação a "t", tem-se:
. Um outro detalhe importantíssimo é reparar que o (pi*x) é constante em relação à t. Logo, derivando parcialmente em relação a "t", tem-se:







