 por Rafael-Miranda » Dom Abr 26, 2015 12:57
por Rafael-Miranda » Dom Abr 26, 2015 12:57
Bom dia!
Gostaria de pedir a ajuda de alguém para resolver essa questão.
Antes de mais nada, gostaria de dizer que se trata de provar o limite por épsilon e delta.
Estou tendo uma dificuldade enorme, pois envolve restrição de intervalo e eu ainda não consegui compreender essa parte do assunto.
Aqui vai: limite de 9/x+1 quando x tende a 2=3
Comecei assim: Queremos provar que para todo £>0, existe um s>0 tal que 0<x-2<s, então 9/x+1 -3< £.
|(9/x+1) -3| < £ ==> |9-3x-3/x+1| < £ ==>|-3x + 6/x+1| < £ ==> |-3(x-2)/x+1| < £
Como na desigualdade há (x+1) do qual nada se conhece, necessita-se restringir s de modo que encontremos um desigualdade envolvendo-o.
Tomei s < ou = 1 e fiz: -s< x-2 < s ===> -s+2 < x < s+2 ===> 1< x < 3
logo 2< x+1 < 4
Agora, se 0< x-2 < s e x+1<4 , então:
|-3(x-2)/x+1| < 4s ===> |-3| |x-2/x+1| <4s
Nessa parte foi que eu travei. Não sei se em alguma parte eu errei.
Por favor, me ajudem.
Caso possam explicar um pouco sobre como proceder no caso de se fazer necessário restringir, eu iria agradecer muito.
-
Rafael-Miranda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Abr 26, 2015 12:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Engenharia Química
- Andamento: cursando
 por e8group » Dom Abr 26, 2015 19:33
por e8group » Dom Abr 26, 2015 19:33
A ideia a princípio é escolhermos delta positivo de modo a minorar

por um numero positivo , por conseguinte majoraremos
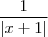
.
Observe que se
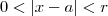
então
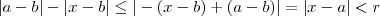
donde tem-se
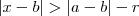
, substituindo a e b pelos valores em interesse , vamos obter
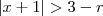
. Veja que sempre que tomarmos 0<r <3 , vamos ter a minoração desejada , destes r> 0 , satisfazendo a propriedade , restringiremos tal arbitrariedade , escolhendo-se um particular(aqui é o nosso

) para cada

dado, de modo que

sempre que

.
Como de costume , vamos rascunhar , estimar o quao pequeno deve ser o delta ... (A organização das ideias e formalização fica como exercício p vc )
Ora ,
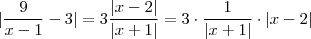
. Assim, se

, vamos ter
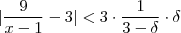
. Gostaríamos que delta fosse tal que

, e sendo temos ,
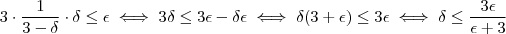
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Rafael-Miranda » Dom Abr 26, 2015 20:01
por Rafael-Miranda » Dom Abr 26, 2015 20:01
Perdão. Mas eu não compreendi a metade superior da explicação. Somente compreendi algo a partir do momento de inserção do f(x).
-
Rafael-Miranda
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Abr 26, 2015 12:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Engenharia Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2788 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 7549 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- DUVIDA LIMITES
 por paulovlg » Qua Jun 18, 2014 23:21
por paulovlg » Qua Jun 18, 2014 23:21
- 1 Respostas
- 1805 Exibições
- Última mensagem por e8group

Qui Jun 19, 2014 14:48
Cálculo: Limites, Derivadas e Integrais
-
- [limites] - dúvida
 por natanaelskt » Sáb Jun 28, 2014 09:35
por natanaelskt » Sáb Jun 28, 2014 09:35
- 1 Respostas
- 1394 Exibições
- Última mensagem por e8group

Sáb Jun 28, 2014 13:26
Cálculo: Limites, Derivadas e Integrais
-
- duvida em calculo de limites
por Andersonborges » Dom Abr 03, 2011 20:13
- 7 Respostas
- 5032 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 17:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 por um numero positivo , por conseguinte majoraremos
por um numero positivo , por conseguinte majoraremos 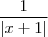 .
. 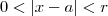 então
então 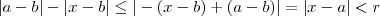 donde tem-se
donde tem-se 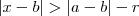 , substituindo a e b pelos valores em interesse , vamos obter
, substituindo a e b pelos valores em interesse , vamos obter 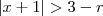 . Veja que sempre que tomarmos 0<r <3 , vamos ter a minoração desejada , destes r> 0 , satisfazendo a propriedade , restringiremos tal arbitrariedade , escolhendo-se um particular(aqui é o nosso
. Veja que sempre que tomarmos 0<r <3 , vamos ter a minoração desejada , destes r> 0 , satisfazendo a propriedade , restringiremos tal arbitrariedade , escolhendo-se um particular(aqui é o nosso  ) para cada
) para cada  dado, de modo que
dado, de modo que  sempre que
sempre que  .
. 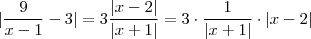 . Assim, se
. Assim, se  , vamos ter
, vamos ter 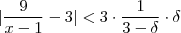 . Gostaríamos que delta fosse tal que
. Gostaríamos que delta fosse tal que  , e sendo temos ,
, e sendo temos , 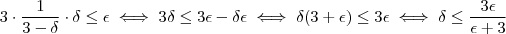 .
.