 por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
Seja
![f(x)= [cos x], -\pi \leq x \leq \pi f(x)= [cos x], -\pi \leq x \leq \pi](/latexrender/pictures/6d2672b0e6524334517a98ed45e26c9b.png)
. (Os colchetes simbolizam a função piso)
a) Calcule cada limite, se existir.
I)
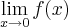
II)

III)
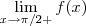
IV)
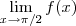
b) Para quais valores de a existe

?
Sei que a função maior inteiro representa o maior inteiro que não ultrapasse o valor de X mas não consigo responder essa questão e não tenho o gabarito. Obrigado desde já!
-
ViniciusAlmeida
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Seg Fev 09, 2015 12:13
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qua Fev 18, 2015 10:56
por adauto martins » Qua Fev 18, 2015 10:56
![f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right] f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right]](/latexrender/pictures/a6654b1aa87894edcc9dbcc4ac19a9a8.png)
por definiçao temos:
![\left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z \left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z](/latexrender/pictures/55ba575bf9c1de38cf4f8c6731589961.png)
,entao
![\left[cox \right]\preceq cosx \prec \left[cosx \right]+1 \left[cox \right]\preceq cosx \prec \left[cosx \right]+1](/latexrender/pictures/13ee90b3145aa84f4c0c9ced41d2a821.png)
logo...I)
![\lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1 \lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1](/latexrender/pictures/b13c775b7b0b4405b61dc46eaba3a38e.png)
II)
![\lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0 \lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0](/latexrender/pictures/6612b303fba0eb51c8b1adf775a0e002.png)
...
o mesmo valor p/III,IV
b)por definiçao

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Fev 19, 2015 15:01
por adauto martins » Qui Fev 19, 2015 15:01
uma correçao:
nao existe o
![\lim_{x\rightarrow a}\left[f(x) \right] \lim_{x\rightarrow a}\left[f(x) \right]](/latexrender/pictures/b9cfe93e359820cd9c7df3519c27f248.png)
,pois p/diferentes valores de x,o limite tem o mesmo valor...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]-Função maior inteiro
por antonioferro » Sáb Fev 13, 2016 15:25
- 0 Respostas
- 2017 Exibições
- Última mensagem por antonioferro

Sáb Fev 13, 2016 15:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1616 Exibições
- Última mensagem por DanielFerreira

Sex Abr 17, 2015 20:32
Funções
-
- Limite de funções
 por jeremiashenrique » Sex Abr 17, 2015 16:07
por jeremiashenrique » Sex Abr 17, 2015 16:07
- 1 Respostas
- 1628 Exibições
- Última mensagem por adauto martins

Seg Abr 20, 2015 20:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= [cos x], -\pi \leq x \leq \pi f(x)= [cos x], -\pi \leq x \leq \pi](/latexrender/pictures/6d2672b0e6524334517a98ed45e26c9b.png) . (Os colchetes simbolizam a função piso)
. (Os colchetes simbolizam a função piso)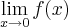

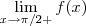
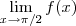
 ?
?

![f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right] f(x)=cosx\Rightarrow \left[f(x) \right]=\left[cosx \right]](/latexrender/pictures/a6654b1aa87894edcc9dbcc4ac19a9a8.png)
![\left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z \left[f(x) \right]\preceq \left[f(x) \right]\prec \left[f(x) \right]+1,p/\left[f(x) \right]\in Z](/latexrender/pictures/55ba575bf9c1de38cf4f8c6731589961.png) ,entao
,entao![\left[cox \right]\preceq cosx \prec \left[cosx \right]+1 \left[cox \right]\preceq cosx \prec \left[cosx \right]+1](/latexrender/pictures/13ee90b3145aa84f4c0c9ced41d2a821.png)
![\lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1 \lim_{x\rightarrow 0}\left[cosx \right]\preceq \lim_{x\rightarrow 0}cosx\prec \lim_{x\rightarrow 0}cosx+1\Rightarrow \lim_{x\rightarrow 0}\left[cosx \right]=cos0=1](/latexrender/pictures/b13c775b7b0b4405b61dc46eaba3a38e.png)
![\lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0 \lim_{x\rightarrow {\pi/2}^{-}}\left[cosx \right]\preceq \lim_{x\rightarrow {\pi/2}^{-}}cosx=cos(\pi/2)=0](/latexrender/pictures/6612b303fba0eb51c8b1adf775a0e002.png) ...
...

![\lim_{x\rightarrow a}\left[f(x) \right] \lim_{x\rightarrow a}\left[f(x) \right]](/latexrender/pictures/b9cfe93e359820cd9c7df3519c27f248.png) ,pois p/diferentes valores de x,o limite tem o mesmo valor...
,pois p/diferentes valores de x,o limite tem o mesmo valor...
 .
.
 :
: