Solicito a vossa ajuda no sentido de resolver um problema de otimização. Não estou a conseguir escrever o modelo matemático para o problema. Sou estudante trabalhador e as aulas são no horário laboral por isso, tenho muitas dificuldades em assistir as mesmas.
O problema é:
" Um agricultor consegue vender 1 kg de batata por 2 u.m no primeiro dia do ano, mas, depois disso, o preço cai a razão de 2 centavos da u.m. por kg ao dia. No dia 1º de Janeiro, um agricultor tem 80 kg de batata no campo e calcula que a produção será aumentada à razão de 1 kg ao dia. Em que dia o agricultor deve colher as suas batatas para maximizar a receita?"
Agradeço desde já a vossa compreensão e fico no aguardo de uma rápida resposta

Neusa


 do kg no dia
do kg no dia  ( contando t=1 como 1° de Jan) é tal que
( contando t=1 como 1° de Jan) é tal que 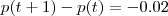 , onde
, onde 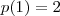
 de batatas no dia
de batatas no dia 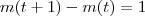 , onde
, onde  .
.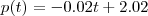


 . Ou seja, a colheita deve ser feita dia 11 de Janeiro.
. Ou seja, a colheita deve ser feita dia 11 de Janeiro.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.