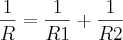 Supondo que R1= 30 ohms e R2 = 50 ohms , calcule a variação de R se:
Supondo que R1= 30 ohms e R2 = 50 ohms , calcule a variação de R se:a) R1 aumenta de 0,03 ohms e R2 diminui de 0,05 ohms
b) R1 diminui de 0,07 ohms e R2 aumenta de 0,04 ohms .
Resp: a) dR = 0,0047 ohms
b) dR = -0,022 ohms
Como chego neste resultado?
Obrigado !


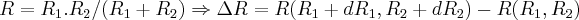 ...
...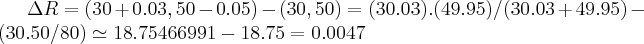
 ,
, 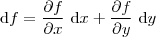 .
.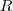 é função das duas resistências
é função das duas resistências 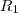 e
e 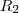 , então
, então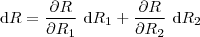 .
.

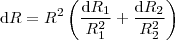
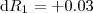 e
e  . Analogamente na letra b).
. Analogamente na letra b).![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)