 por lucas_carvalho » Ter Dez 02, 2014 20:27
por lucas_carvalho » Ter Dez 02, 2014 20:27
Boa noite!
Estou com dúvidas nessa questão retirada do livro "Cálculo" de James Stewart, 7° edição:
Suponha que uma bola de neve derreta de maneira que seu volume decresce a uma taxa proporcional a área de sua superfície. Se levar três horas para a bola de neve derreter para a metade de seu volume original, quanto tempo demorará para a bola de neve derreter completamente?
Obrigado pela atenção

-
lucas_carvalho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Dez 02, 2014 20:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia química
- Andamento: formado
 por adauto martins » Qua Dez 03, 2014 20:09
por adauto martins » Qua Dez 03, 2014 20:09
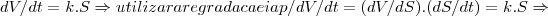
...como

...
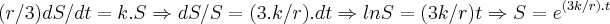
,ou melhor

...
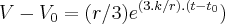
...ai agora e colocar os dados e calcular...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por lucas_carvalho » Qua Dez 03, 2014 20:53
por lucas_carvalho » Qua Dez 03, 2014 20:53
Eu pensei nessa forma de resolução, mas ele não dá nenhum dado além do que eu passei aqui. E a resposta dada no final do livro é 11/2 h
-
lucas_carvalho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Dez 02, 2014 20:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60602 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5492 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10628 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- [Variação Percentual]
por Wilson Rogerio Braun » Sex Ago 26, 2011 21:29
- 4 Respostas
- 4177 Exibições
- Última mensagem por Wilson Rogerio Braun

Seg Ago 29, 2011 13:59
Álgebra Elementar
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8460 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



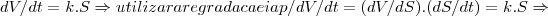 ...como
...como  ...
...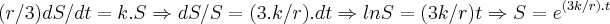 ,ou melhor
,ou melhor  ...
...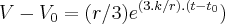 ...ai agora e colocar os dados e calcular...
...ai agora e colocar os dados e calcular...
