 por Vencill » Ter Dez 02, 2014 17:21
por Vencill » Ter Dez 02, 2014 17:21
Boa tarde!
Estou com dúvida no seguinte exercício:
A aresta de um cubo mede 30 cm com um erro de medida de 0,1 cm. Utilizando diferenciais estimar o erro máximo e relativo no cálculo:
a) volume.
b) Área da superfície do cubo.
Dúvida: é o seguinte como tenho um pouco de dificuldade em diferenciais, não consigo resolver este exercício, a resposta da
a é

e 1% e da
b é
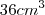
e 0,6%.
Agradeço se alguem me ajudar!
-
Vencill
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Nov 13, 2014 16:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por lucas_carvalho » Ter Dez 02, 2014 21:05
por lucas_carvalho » Ter Dez 02, 2014 21:05
Boa noite!!
Bom, vamos lá. Sabemos que o volume V de um cubo de aresta a é dado por:
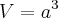
Agora devemos derivar em relação a "a":
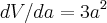
Logo:

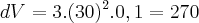
é o erro máximo cometido na medição do volume.
Para calcular o erro percentual, fazemos:
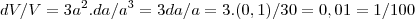
Essa foi a letra "a"
A área da superfície de um cubo é dada por:
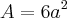
Derivando:

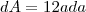
Então o erro máximo na medida é:
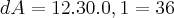
Para o erro percentual:

Essa foi a letra 'b"
Espero ter ajudado, desculpe qualquer erro (é a primeira vez que entro nesse fórum).
-
lucas_carvalho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Dez 02, 2014 20:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia química
- Andamento: formado
 por Vencill » Qua Dez 03, 2014 16:22
por Vencill » Qua Dez 03, 2014 16:22
Nossa obrigado mesmo!!
-
Vencill
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Nov 13, 2014 16:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo Diferencial] Diferenciais para estimar erro máximo
por wandeng » Sáb Abr 29, 2017 15:48
- 0 Respostas
- 4145 Exibições
- Última mensagem por wandeng

Sáb Abr 29, 2017 15:48
Cálculo: Limites, Derivadas e Integrais
-
- dúvida erro relativo
por daniloadanilo » Dom Set 12, 2010 22:29
- 0 Respostas
- 1605 Exibições
- Última mensagem por daniloadanilo

Dom Set 12, 2010 22:29
Cálculo: Limites, Derivadas e Integrais
-
- maximo e minimos relativo
por matematica_mat » Sáb Out 29, 2011 13:05
- 0 Respostas
- 1737 Exibições
- Última mensagem por matematica_mat

Sáb Out 29, 2011 13:05
Cálculo Numérico e Aplicações
-
- [ Equação de 3º Grau ] Encontrar valor de máximo relativo
por Fabio Ribeiro » Qui Jun 05, 2014 12:30
- 4 Respostas
- 8857 Exibições
- Última mensagem por Fabio Ribeiro

Sáb Jun 07, 2014 18:56
Funções
-
- Risco relativo
por gustavomonj » Sex Mar 25, 2011 01:30
- 1 Respostas
- 2051 Exibições
- Última mensagem por Neperiano

Sex Out 21, 2011 16:16
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e 1% e da b é
e 1% e da b é 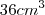 e 0,6%.
e 0,6%.

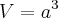
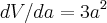

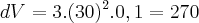 é o erro máximo cometido na medição do volume.
é o erro máximo cometido na medição do volume. 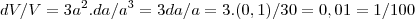
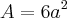

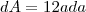
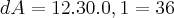


 .
.



