Boa tarde,
gostaria de pedir ajuda para entender como se identifica a tendencia deste limite.
Obrigado



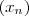 é convergente para
é convergente para  , então dado
, então dado 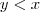 existe
existe 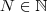 tal que
tal que 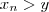 . Prova :
. Prova : 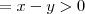 e usar a definição de convergência de sequência .
e usar a definição de convergência de sequência .  . Note que a sequência
. Note que a sequência 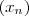 é convergente para
é convergente para  .Daí , dado
.Daí , dado  ,aplicando o lemma , temos a existência de
,aplicando o lemma , temos a existência de  tal que
tal que  e assim
e assim 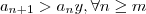 (pois a_n > 0 ) . Veja que
(pois a_n > 0 ) . Veja que 
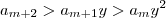
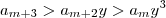
 .
. , temos
, temos 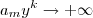 e por isso
e por isso 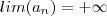 . Caso queira mais rigor , faremos o seguinte , você propõe um número arbitrário , grande o quanto você queira, e mostraremos que a sequência
. Caso queira mais rigor , faremos o seguinte , você propõe um número arbitrário , grande o quanto você queira, e mostraremos que a sequência 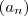 contém infinitamente muitos termos (de índices consecutivos ) que excede este número escolhido ... traduzindo
contém infinitamente muitos termos (de índices consecutivos ) que excede este número escolhido ... traduzindo  .
.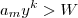 temos
temos 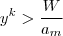 implicando
implicando 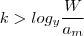 (pois
(pois  ) . Seja então
) . Seja então  o menor inteiro positivo que satisfaz esta desigualdade (P.S.: a existência de k_o é assegurada pela pela propriedade Arquimediana ) .Daí , para qualquer índice
o menor inteiro positivo que satisfaz esta desigualdade (P.S.: a existência de k_o é assegurada pela pela propriedade Arquimediana ) .Daí , para qualquer índice 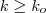 temos
temos 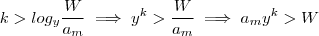 .
.  . Logo , por transitividade ,
. Logo , por transitividade , 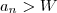 (com
(com  ) sempre que
) sempre que 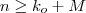 o que prova formalmente que o limite da sequência
o que prova formalmente que o limite da sequência 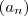 diverge para
diverge para  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

