 por Gustavooguto » Qua Nov 12, 2014 09:30
por Gustavooguto » Qua Nov 12, 2014 09:30
Bom dia
Preciso encontrar o limite dessa função, mas TENHO que aplicar L'Hospital e não sei como fazer isso pois tem que "arrumar" a função.

obrigado
-
Gustavooguto
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 17, 2014 10:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por adauto martins » Qua Nov 12, 2014 12:25
por adauto martins » Qua Nov 12, 2014 12:25
regra de l'hospital aplica-se em casos de indeterminaçoes de limites
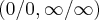
em sua maiorias das vezes,e tambem em outros casos como

depois se fazer certas manipulaçoes algebricas em limites(qquer livro de calculo,encontra-se)...a regra eh:
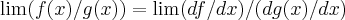
...

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida de L'hospital em função trigonométrica composta
por Thamc » Sex Dez 02, 2011 19:26
- 1 Respostas
- 1032 Exibições
- Última mensagem por LuizAquino

Sáb Dez 03, 2011 12:17
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por cal12 » Sáb Nov 26, 2011 17:52
- 1 Respostas
- 1682 Exibições
- Última mensagem por LuizAquino

Sáb Nov 26, 2011 18:13
Cálculo: Limites, Derivadas e Integrais
-
- l'hospital
por vinicastro » Dom Dez 16, 2012 16:32
- 1 Respostas
- 1520 Exibições
- Última mensagem por vinicastro

Dom Dez 16, 2012 17:15
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por matmatco » Sáb Fev 23, 2013 16:35
- 1 Respostas
- 1632 Exibições
- Última mensagem por LuizAquino

Ter Fev 26, 2013 17:09
Cálculo: Limites, Derivadas e Integrais
-
- L'Hospital
por duduxo81 » Sex Jul 08, 2016 11:30
- 3 Respostas
- 5275 Exibições
- Última mensagem por duduxo81

Qua Jul 13, 2016 11:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




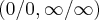 em sua maiorias das vezes,e tambem em outros casos como
em sua maiorias das vezes,e tambem em outros casos como  depois se fazer certas manipulaçoes algebricas em limites(qquer livro de calculo,encontra-se)...a regra eh:
depois se fazer certas manipulaçoes algebricas em limites(qquer livro de calculo,encontra-se)...a regra eh: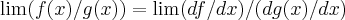 ...
... ...
...