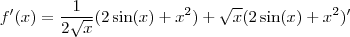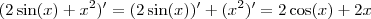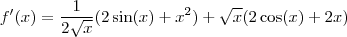Isto é uma função e não uma equação! Cuidado.
Primeiro, você aplica a regra do produto. Note que a sua função é
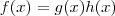
,onde

e

. Concorda? Então, a derivada da função

,que vamos denotar por

, é
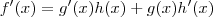
A famosa " Derivada-da-primeira-vezes-a-segunda-mais-a-primeira-vezes-a-derivada-da-segunda". Você já deve ter visto essa fórmula.
Daí, como
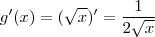
, então
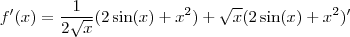
Agora, como a derivada de uma soma é a soma das derivadas, fazemos
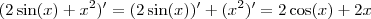
e então,
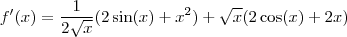
Ok? Agora pode rearranjar os termos se quiser.
![f(x)=\sqrt[]{x} * (2Senx + {x}^{2}) f(x)=\sqrt[]{x} * (2Senx + {x}^{2})](/latexrender/pictures/20bfa732e066eaa6146b62d3edffdedb.png)

![f(x)=\sqrt[]{x} * (2Senx + {x}^{2}) f(x)=\sqrt[]{x} * (2Senx + {x}^{2})](/latexrender/pictures/20bfa732e066eaa6146b62d3edffdedb.png)

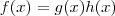 ,onde
,onde  e
e  . Concorda? Então, a derivada da função
. Concorda? Então, a derivada da função  ,que vamos denotar por
,que vamos denotar por  , é
, é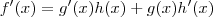
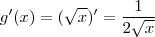 , então
, então