 por Fernandobertolaccini » Seg Nov 03, 2014 17:36
por Fernandobertolaccini » Seg Nov 03, 2014 17:36
Resolver:
![\int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2} \int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2}](/latexrender/pictures/ed8e2929b06adf5de6561330aba51919.png)
Resp:
![-\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C -\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C](/latexrender/pictures/58fd5ffcd2476198a94b74659994c2f9.png)
Muito Obrigado !!!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por adauto martins » Qui Nov 06, 2014 15:16
por adauto martins » Qui Nov 06, 2014 15:16
faz-se
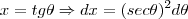
...
![\int_{}^{}\sqrt[]{({tg\theta})^{2}+1})({sec\theta})^{2}d\theta/(({tg\theta})^{2})=\int_{}^{}(sec\theta)})({sec\theta})^{2}d\theta/({tg\theta})^{2} \int_{}^{}\sqrt[]{({tg\theta})^{2}+1})({sec\theta})^{2}d\theta/(({tg\theta})^{2})=\int_{}^{}(sec\theta)})({sec\theta})^{2}d\theta/({tg\theta})^{2}](/latexrender/pictures/deb0127f228c671febde24e440fa7a7f.png)
=
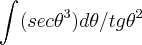
=
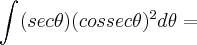
;integrando por partes tal q.

...

...
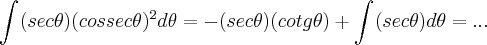
...alguns algebrismo e refazendo as substituiçoes em x,chega-se ao resultado...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3750 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao trigonometrica 3
por beel » Dom Nov 27, 2011 18:24
- 3 Respostas
- 2890 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:44
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2059 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1482 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição Trigonométrica
por klueger » Qua Mar 06, 2013 23:03
- 4 Respostas
- 3653 Exibições
- Última mensagem por Russman

Qui Mar 07, 2013 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2} \int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2}](/latexrender/pictures/ed8e2929b06adf5de6561330aba51919.png)
![-\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C -\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C](/latexrender/pictures/58fd5ffcd2476198a94b74659994c2f9.png)

![\int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2} \int_{}^{}\frac{\sqrt[]{x^2+1}}{x^2}](/latexrender/pictures/ed8e2929b06adf5de6561330aba51919.png)
![-\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C -\frac{\sqrt[]{1+x^2}}{x} + ln(\sqrt[]{1+x^2}+x) + C](/latexrender/pictures/58fd5ffcd2476198a94b74659994c2f9.png)

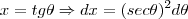 ...
...![\int_{}^{}\sqrt[]{({tg\theta})^{2}+1})({sec\theta})^{2}d\theta/(({tg\theta})^{2})=\int_{}^{}(sec\theta)})({sec\theta})^{2}d\theta/({tg\theta})^{2} \int_{}^{}\sqrt[]{({tg\theta})^{2}+1})({sec\theta})^{2}d\theta/(({tg\theta})^{2})=\int_{}^{}(sec\theta)})({sec\theta})^{2}d\theta/({tg\theta})^{2}](/latexrender/pictures/deb0127f228c671febde24e440fa7a7f.png) =
=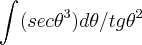 =
=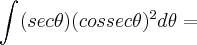 ;integrando por partes tal q.
;integrando por partes tal q.  ...
... ...
...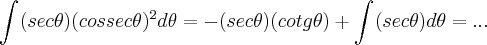 ...alguns algebrismo e refazendo as substituiçoes em x,chega-se ao resultado...
...alguns algebrismo e refazendo as substituiçoes em x,chega-se ao resultado...