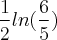por Fernandobertolaccini » Seg Jul 21, 2014 19:46
por Fernandobertolaccini » Seg Jul 21, 2014 19:46
Calcule:

resp:

Muito obrigado
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por jeff_95 » Sex Ago 29, 2014 06:14
por jeff_95 » Sex Ago 29, 2014 06:14
Nessa integral devemos aplicar o método das frações parciais. Para isso devemos verificar se o polinômio pode ser fatorado num produto de binômios. Nesse caso, é fácil fazer isso pois é um polinômio de segundo grau. Após verificar o valor do discriminante

e encontrar as raízes temos que:
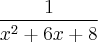
=

Logo é possível separar o termo em 2 frações parcias. Fazendo isso temos:

=

+

Temos que ter:
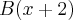
+

= 1 (Polinômios idênticos)
Resolvendo o sistema encontramos:
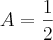
e

Então:

=

=
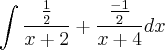
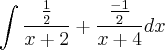
=
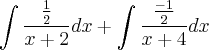
Resolvendo a última integral por substituição (substiuindo u =

e repetindo o mesmo procedimento para a outra integral, temos:

=

Assim

=
![\frac{1}{2}[ln(1+2)-ln(1+4)-ln(0+2)+ln(0+4)] \frac{1}{2}[ln(1+2)-ln(1+4)-ln(0+2)+ln(0+4)]](/latexrender/pictures/c878a949f60e90490e5ac29a4a004537.png)
=
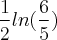
Espero ter ajudado !!
-
jeff_95
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Nov 16, 2013 19:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por Frações Parciais
por Bruhh » Qua Set 29, 2010 18:20
- 2 Respostas
- 5402 Exibições
- Última mensagem por Bruhh

Qui Set 30, 2010 08:40
Cálculo: Limites, Derivadas e Integrais
-
- [integral] fraçoes parciais
por ewald » Qui Set 08, 2011 15:10
- 1 Respostas
- 2112 Exibições
- Última mensagem por Neperiano

Qui Set 08, 2011 15:47
Cálculo: Limites, Derivadas e Integrais
-
- integral frações parciais
por paolaads » Seg Out 22, 2012 21:08
- 3 Respostas
- 2471 Exibições
- Última mensagem por MarceloFantini

Ter Out 23, 2012 18:56
Cálculo: Limites, Derivadas e Integrais
-
- Integral com fracões parciais
por menino de ouro » Dom Nov 25, 2012 17:29
- 4 Respostas
- 3231 Exibições
- Última mensagem por menino de ouro

Dom Nov 25, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral com fracões parciais
por menino de ouro » Seg Nov 26, 2012 21:43
- 1 Respostas
- 1681 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 00:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 e encontrar as raízes temos que:
e encontrar as raízes temos que: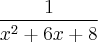 =
= 
 =
=  +
+ 
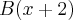 +
+  = 1 (Polinômios idênticos)
= 1 (Polinômios idênticos)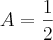 e
e 
 =
=  =
= 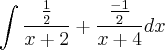
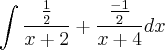 =
= 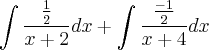
 e repetindo o mesmo procedimento para a outra integral, temos:
e repetindo o mesmo procedimento para a outra integral, temos: =
= 
 =
= ![\frac{1}{2}[ln(1+2)-ln(1+4)-ln(0+2)+ln(0+4)] \frac{1}{2}[ln(1+2)-ln(1+4)-ln(0+2)+ln(0+4)]](/latexrender/pictures/c878a949f60e90490e5ac29a4a004537.png) =
=