![\displaystyle \int \sqrt[4]{\tan x}dx \displaystyle \int \sqrt[4]{\tan x}dx](/latexrender/pictures/dc8f98b38a94c51f80a1c94db7fc222b.png)


![\displaystyle \int \sqrt[4]{\tan x}dx \displaystyle \int \sqrt[4]{\tan x}dx](/latexrender/pictures/dc8f98b38a94c51f80a1c94db7fc222b.png)

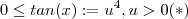 . Taking a derivative from both sides of
. Taking a derivative from both sides of  , we get
, we get 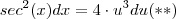 . Now , we use an identity to give an expression a more convenient form
. Now , we use an identity to give an expression a more convenient form 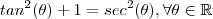 .Thus
.Thus 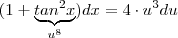 which yields
which yields 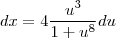 . And finally we have ,
. And finally we have , ![\int \sqrt[4]{tan(x)} dx = 4 \int \frac{u^4}{1+u^8} du \int \sqrt[4]{tan(x)} dx = 4 \int \frac{u^4}{1+u^8} du](/latexrender/pictures/d4e5f45ad7247613c937846a5ae19cbf.png) .
. 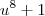 as a
as a 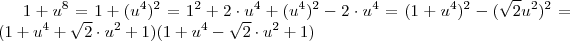

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes