 por Daniela[ » Sáb Jul 05, 2014 15:15
por Daniela[ » Sáb Jul 05, 2014 15:15
Boa Tarde
Estou com dúvida em duas resoluções de problemas envolvendo taxas relacionadas, gostaria de um auxílio!
1- O ar está sendo bombeado para dentro de um balão esférico á taxa de 4,5 polegadas cúbicas por minuto. Ache a taxa de variação do raio quando este é de 2 polegadas. Lembrando que o volume da esfera é dado por V= 4pir³/3.
2- Uma pedra cai livremente em um lago parado. Ondas circulares se espalham e o raio da região afetada aumenta a uma taxa de 16cm/s. Qual a taxa de variação da área em relação ao tempo, quando o raio da região for de 4cm? (A=pir²)
NO AGUARDO!
OBRIGADA
-
Daniela[
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 05, 2014 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia quimica
- Andamento: cursando
 por young_jedi » Sáb Jul 05, 2014 15:34
por young_jedi » Sáb Jul 05, 2014 15:34
derivando o volume com relação ao tempo teremos
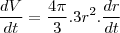

como a taxa de variação do volume é igual a taxa de ar que esta sendo bombeado
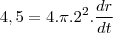
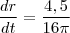
a segunda equação é parecida é só derivar e substituir valores tente concluir e comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Daniela[ » Dom Jul 06, 2014 11:30
por Daniela[ » Dom Jul 06, 2014 11:30
Bom dia!
Obrigada consegui intender e fazer, e cheguei no resultado que tenho aqui 0,09 pol/min.
E a outra você conseguiria me auxiliar, tenho a resposta de 128 pi cm²/s, mais tentei e não chego no raciocinio correto, se poderes me auxiliar!
Muito Obrigada!
-
Daniela[
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 05, 2014 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia quimica
- Andamento: cursando
 por young_jedi » Dom Jul 06, 2014 14:25
por young_jedi » Dom Jul 06, 2014 14:25
Tudo bem
Utilizando a equação da area
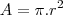
derivando de maneira implicita com relação ao tempo
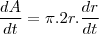
como

para r=4 teriamos
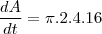

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Taxas Relacionadas]
por Ana_Rodrigues » Seg Nov 14, 2011 10:02
- 2 Respostas
- 4593 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 12:19
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:48
- 0 Respostas
- 1462 Exibições
- Última mensagem por RonnieAlmeida

Qui Mai 22, 2014 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Taxas Relacionadas
por RonnieAlmeida » Qui Mai 22, 2014 16:58
- 1 Respostas
- 2710 Exibições
- Última mensagem por alienante

Dom Jun 15, 2014 07:59
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Lorijuca » Qui Mai 29, 2014 22:23
- 0 Respostas
- 2954 Exibições
- Última mensagem por Lorijuca

Qui Mai 29, 2014 22:23
Cálculo: Limites, Derivadas e Integrais
-
- Taxas relacionadas
por Fernandobertolaccini » Sáb Out 25, 2014 09:57
- 5 Respostas
- 4577 Exibições
- Última mensagem por Fernandobertolaccini

Sáb Out 25, 2014 12:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


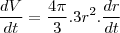

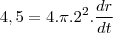
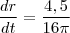

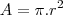
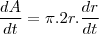
 para r=4 teriamos
para r=4 teriamos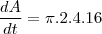

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)