a questão é a seguinte:
![f(x)=[sen(x)]^{[2x^x-x+3]} f(x)=[sen(x)]^{[2x^x-x+3]}](/latexrender/pictures/c203a533d1249fa3a0bd9482a780bfc4.png)
comecei levando em consideração, primeiramente, a derivação de

tendo como v=
![[2x^x-x+3] [2x^x-x+3]](/latexrender/pictures/fd3b4e310353318714e0a6def73e93be.png) , e posteriormente a de "v". Entretanto, o problema, acredito, esta realmente na derivação de
, e posteriormente a de "v". Entretanto, o problema, acredito, esta realmente na derivação de  . Pois o expoente da expressão, no gabarito, está bem diferente o meu.
. Pois o expoente da expressão, no gabarito, está bem diferente o meu.Eis a resposta que encontrei e a do gabarito, respectivamente:
![(2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x)) (2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x))](/latexrender/pictures/9dd6a1e33c1b82de7ba2309faddc6e34.png)
e
![{[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]} {[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]}](/latexrender/pictures/b10b5610012742c7f7da39e0e5c6d7fa.png)
Alguém poderia me ajudar? Mto Obrigada


 ?
?  , para tal, note que
, para tal, note que 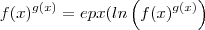 ( Aqui usamos que epx composta com ln dá a aplicação identidade e vice-versa ) .
( Aqui usamos que epx composta com ln dá a aplicação identidade e vice-versa ) . 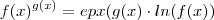 .
.  em
em  .Agora é possível derivar
.Agora é possível derivar 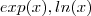 e temos a regra da cadeia e produto .
e temos a regra da cadeia e produto . 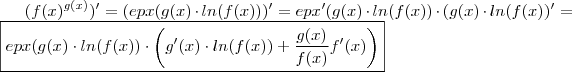
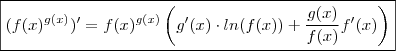


 .
.



