 por anner » Sex Jul 04, 2014 00:14
por anner » Sex Jul 04, 2014 00:14
Boa noite, pessoal. Tô com uma certa dificuldade numa derivada aqui, já quebrei a cabeça aqui e não consigo chegar a resposta do gabarito.
a questão é a seguinte:
![f(x)=[sen(x)]^{[2x^x-x+3]} f(x)=[sen(x)]^{[2x^x-x+3]}](/latexrender/pictures/c203a533d1249fa3a0bd9482a780bfc4.png)
comecei levando em consideração, primeiramente, a derivação de

tendo como v=
![[2x^x-x+3] [2x^x-x+3]](/latexrender/pictures/fd3b4e310353318714e0a6def73e93be.png)
, e posteriormente a de "v". Entretanto, o problema, acredito, esta realmente na derivação de

. Pois o expoente da expressão, no gabarito, está bem diferente o meu.
Eis a resposta que encontrei e a do gabarito, respectivamente:
![(2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x)) (2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x))](/latexrender/pictures/9dd6a1e33c1b82de7ba2309faddc6e34.png)
e
![{[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]} {[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]}](/latexrender/pictures/b10b5610012742c7f7da39e0e5c6d7fa.png)
Alguém poderia me ajudar? Mto Obrigada

-
anner
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jul 03, 2014 23:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Sex Jul 04, 2014 01:17
por e8group » Sex Jul 04, 2014 01:17
Como derivar expressões da forma

?
A dica é escrever

na base

, para tal, note que
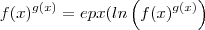
( Aqui usamos que epx composta com ln dá a aplicação identidade e vice-versa ) .
Utilizando propriedades de logaritmo , segue-se que
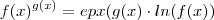
.
Observe que estamos avaliando

em

.Agora é possível derivar

pois conhecemos a derivada de
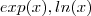
e temos a regra da cadeia e produto .
Aplicando a regra da cadeia e regra do produto obterá
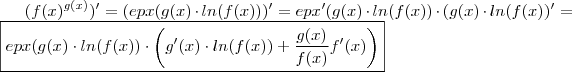
Ou se preferir
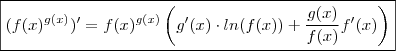
Recomendo que tente fazer o exercício seguindo o mesmo raciocínio .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Daniela[ » Sáb Jul 05, 2014 14:40
por Daniela[ » Sáb Jul 05, 2014 14:40
Boa Tarde!
Estou com dúvida em duas resoluções de problemas envolvendo taxas relacionadas, gostaria de um auxílio!
1- O ar está sendo bombeado para dentro de um balão esférico á taxa de 4,5 polegadas cúbicas por minuto. Ache a taxa de variação do raio quando este é de 2 polegadas. Lembrando que o volume da esfera é dado por V= 4pir³/3.
2- Uma pedra cai livremente em um lago parado. Ondas circulares se espalham e o raio da região afetada aumenta a uma taxa de 16cm/s. Qual a taxa de variação da área em relação ao tempo, quando o raio da região for de 4cm? (A=pir²)
NO AGUARDO!
OBRIGADA
-
Daniela[
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 05, 2014 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia quimica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Regra da cadeia
por gabriel feron » Seg Out 01, 2012 23:08
- 1 Respostas
- 1594 Exibições
- Última mensagem por young_jedi

Seg Out 01, 2012 23:16
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] regra da cadeia
por tatianaCAL » Sáb Jun 22, 2013 09:47
- 1 Respostas
- 1501 Exibições
- Última mensagem por young_jedi

Sáb Jun 22, 2013 11:33
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]regra da cadeia
por principiante » Dom Fev 04, 2018 10:28
- 1 Respostas
- 5047 Exibições
- Última mensagem por Baltuilhe

Dom Fev 04, 2018 21:02
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela regra da cadeia
por Priscila_moraes » Ter Dez 06, 2011 12:48
- 3 Respostas
- 3005 Exibições
- Última mensagem por MarceloFantini

Ter Dez 06, 2011 15:38
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada - Regra da cadeia
por Sobreira » Dom Dez 02, 2012 13:23
- 1 Respostas
- 2458 Exibições
- Última mensagem por DanielFerreira

Dom Dez 02, 2012 18:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=[sen(x)]^{[2x^x-x+3]} f(x)=[sen(x)]^{[2x^x-x+3]}](/latexrender/pictures/c203a533d1249fa3a0bd9482a780bfc4.png)

![[2x^x-x+3] [2x^x-x+3]](/latexrender/pictures/fd3b4e310353318714e0a6def73e93be.png) , e posteriormente a de "v". Entretanto, o problema, acredito, esta realmente na derivação de
, e posteriormente a de "v". Entretanto, o problema, acredito, esta realmente na derivação de  . Pois o expoente da expressão, no gabarito, está bem diferente o meu.
. Pois o expoente da expressão, no gabarito, está bem diferente o meu.![(2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x)) (2x^x-x+3){[sen(x)]^{[2x^x-x+2]}}cos(x)+{[sen(x)]^{[2x^x-x+3]}}ln[sen(x)](2x^x)[1+ln(x)]-{[sen(x)]^{[2x^x-x+3]}}ln(sen(x))](/latexrender/pictures/9dd6a1e33c1b82de7ba2309faddc6e34.png)
![{[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]} {[sen(x)]^{[2x^x-x+3]}}{[2x^x]-x+3}cotg(x)+ln[sen(x)][2x^x(ln(x)+1)-1]}](/latexrender/pictures/b10b5610012742c7f7da39e0e5c6d7fa.png)


 ?
?  , para tal, note que
, para tal, note que 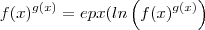 ( Aqui usamos que epx composta com ln dá a aplicação identidade e vice-versa ) .
( Aqui usamos que epx composta com ln dá a aplicação identidade e vice-versa ) . 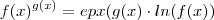 .
.  em
em  .Agora é possível derivar
.Agora é possível derivar 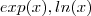 e temos a regra da cadeia e produto .
e temos a regra da cadeia e produto . 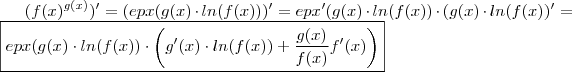
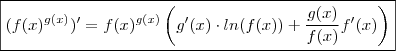



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.