 por Marcos07 » Seg Jun 30, 2014 01:34
por Marcos07 » Seg Jun 30, 2014 01:34
Eu consigo compreender bem os exercícios de aplicação desses limites, mas estou com bastante dificuldade em teoremas desse gênero.
Editado pela última vez por
Marcos07 em Ter Jul 01, 2014 01:28, em um total de 1 vez.
-
Marcos07
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 30, 2014 01:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Seg Jun 30, 2014 02:36
por e8group » Seg Jun 30, 2014 02:36
Vamos tentar por permanência do sinal . Tomemos como axioma que
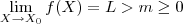
existe . Formalmente (espero não estar a errar com as definições ... ) isso equivale dizer ,
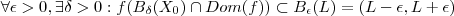
.
Tome
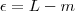
, existe

correspondente t.q
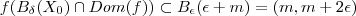
.
Deixe em particular m = 0 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão Aberta da UERJ 2005 ! Me ajudem Por favor !
por Domingues » Qua Out 08, 2008 13:52
- 1 Respostas
- 4666 Exibições
- Última mensagem por admin

Ter Out 14, 2008 16:26
Trigonometria
-
- Bola de beisebol
por Cleyson007 » Qua Nov 07, 2012 16:55
- 7 Respostas
- 8793 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:00
Física
-
- Lançamento de uma bola
por Cleyson007 » Sex Nov 09, 2012 20:25
- 2 Respostas
- 1841 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 22:44
Física
-
- Queda de uma bola em Progressão
por Carolziiinhaaah » Qua Jun 16, 2010 12:02
- 1 Respostas
- 1697 Exibições
- Última mensagem por Elcioschin

Qua Jun 16, 2010 13:38
Progressões
-
- Prove que a bola está no saco
por joaofonseca » Sáb Mar 03, 2012 20:31
- 5 Respostas
- 3291 Exibições
- Última mensagem por Guill

Sáb Mar 17, 2012 14:00
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



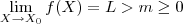 existe . Formalmente (espero não estar a errar com as definições ... ) isso equivale dizer ,
existe . Formalmente (espero não estar a errar com as definições ... ) isso equivale dizer , 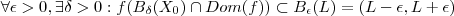 .
. 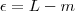 , existe
, existe  correspondente t.q
correspondente t.q 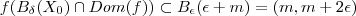 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.