 onde |t|< 1 então
onde |t|< 1 então 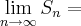 :
:a) 1;
b)
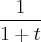 ;
;c)
 ;
;d) 1 - t;
e)
 .
.
 onde |t|< 1 então
onde |t|< 1 então 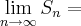 :
: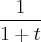 ;
; ;
; .
.

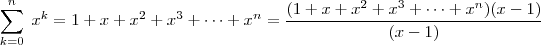
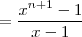
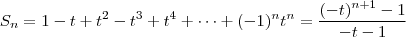

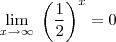 , bastar ver no gráfico da função exponencial quando a base é entre 0 e 1 a função tende a zero quando x tende a mais infinito.
, bastar ver no gráfico da função exponencial quando a base é entre 0 e 1 a função tende a zero quando x tende a mais infinito.
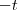 . Quando
. Quando 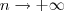 , o estudo em interesse é sobre série geométrica . Dada qualquer P.G. , sempre é possível escrever a soma dos
, o estudo em interesse é sobre série geométrica . Dada qualquer P.G. , sempre é possível escrever a soma dos  primeiros termos em função do termo de índice
primeiros termos em função do termo de índice  e a dedução da mesma não é tão complicada assim . Para inicio de conversar , fixa
e a dedução da mesma não é tão complicada assim . Para inicio de conversar , fixa 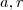 qualquer com
qualquer com  . Agora , defina a sequência geométrica
. Agora , defina a sequência geométrica  (aq incluindo o zero) com
(aq incluindo o zero) com  e
e 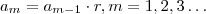 (Aq ganhamos recursividade) ou se você preferir , (o que é ideal p/ soma dos termos )
(Aq ganhamos recursividade) ou se você preferir , (o que é ideal p/ soma dos termos )  . A soma dos
. A soma dos  primeiros termos se dá por
primeiros termos se dá por 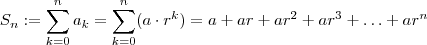 .
.  em comum ; deixando este numero em evidência , segue
em comum ; deixando este numero em evidência , segue  .
.  primeiros termos da P.G. , ou seja ,
primeiros termos da P.G. , ou seja , 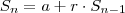 . Mas ,
. Mas , 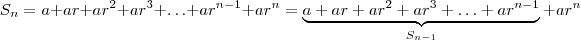 o que implica que
o que implica que 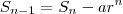 . Logo ,
. Logo ,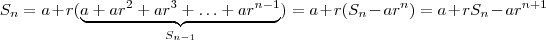 .
.  temos
temos 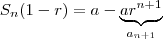
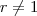 temos que
temos que 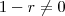 , podemos então dividir ambos membros por
, podemos então dividir ambos membros por  e obter a fórmula
e obter a fórmula 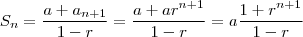 .
. pelo limite
pelo limite  .
.  então
então 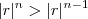 . Por mais que seja grande
. Por mais que seja grande 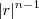 (para n suficiente grande )
(para n suficiente grande )  ; logo
; logo 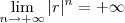 .
. 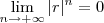 ) (pq ??) .
) (pq ??) .  sempre que
sempre que  .
.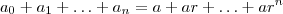 com
com 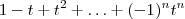 temos
temos 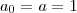 e
e 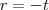 .Como
.Como  por definição então o limite de
por definição então o limite de  é ...
é ... ![\sum [f(x)]^k \sum [f(x)]^k](/latexrender/pictures/957777f5daad88bcd2080b7ec1311d7c.png) a soma dos termos de uma P.G . correspondente .
a soma dos termos de uma P.G . correspondente .
 e
e 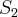 . Sendo assim
. Sendo assim  fica igual a:
fica igual a:  para |t|< 1, com
para |t|< 1, com  =
= 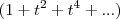 e
e 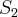 =
= 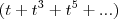 .
. e
e 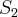 são iguais ao somatório da P.G. Logo,
são iguais ao somatório da P.G. Logo, 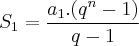 e
e 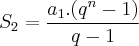 ; substituindo os primeiros termos dos dois somatórios e a razão, temos:
; substituindo os primeiros termos dos dois somatórios e a razão, temos: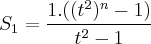 e
e 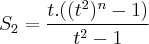 , para
, para  com primeiro termo
com primeiro termo  e para
e para 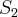 com primeiro termo igual a t e com razão igual a
com primeiro termo igual a t e com razão igual a  .
.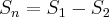 , isso implica que:
, isso implica que:![{S}_{n}=\left[\frac{1.((t^2)^n-1)}{t^2-1}-\frac{t.((t^2)^n-1)}{t^2-1} \right] {S}_{n}=\left[\frac{1.((t^2)^n-1)}{t^2-1}-\frac{t.((t^2)^n-1)}{t^2-1} \right]](/latexrender/pictures/95c38f7ee7671b5cb8a31cec89c72c77.png)

![{S}_{n}=\left[\frac{((t^2)^n-1).(1-t)}{(t-1).(t+1)} \right] {S}_{n}=\left[\frac{((t^2)^n-1).(1-t)}{(t-1).(t+1)} \right]](/latexrender/pictures/2ff1a1f980b9d4abab01ce84a9e13db8.png) =
=![{S}_{n}=\left[\frac{((t^2)^n-1).(1-t)}{-(1-t).(t+1)} \right] {S}_{n}=\left[\frac{((t^2)^n-1).(1-t)}{-(1-t).(t+1)} \right]](/latexrender/pictures/7857d1dd93efdfc3d18f543d6df5ff52.png) =
=![{S}_{n}=\left[\frac{((t^2)^n-1)}{-(t+1)} \right] {S}_{n}=\left[\frac{((t^2)^n-1)}{-(t+1)} \right]](/latexrender/pictures/6fa3a8df61504061091b84e939b10ba9.png) , como |t|<1
, como |t|<1 
 <1, como
<1, como 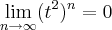 , conclui-se que:
, conclui-se que: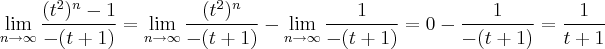 . Está correto?
. Está correto?
 n=1,2,3... ; não pode ter
n=1,2,3... ; não pode ter  e
e 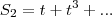 . Note que a cada
. Note que a cada  natural associamos um
natural associamos um  e
e  é único quando
é único quando  é a soma n primeiros termos de uma P.G ou (n+1 primeiros termos caso o °1° termo é de índice 0 ) . Mas em geral não pode se afirma que é único .
é a soma n primeiros termos de uma P.G ou (n+1 primeiros termos caso o °1° termo é de índice 0 ) . Mas em geral não pode se afirma que é único .

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes