 por NathBitencourt » Qua Jun 18, 2014 22:59
por NathBitencourt » Qua Jun 18, 2014 22:59
Dada a função

determine:
a) A variação da função
b) Máximos e Mínimos
Assim, eu fiz essa questão em minha prova semestral. Eu derivei e cheguei em:
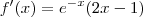
. Só que a partir dai eu não consegui fazer mais nada! Depois de chegar em casa eu continuei a tentar e não conseguia resolver. Depois de desistir eu fui procurar no google para ver se achava algo em relação a isso e eu só acho questões usando integrais (matéria que a gente não viu ainda).
Como ficaram essas respostas sem usar integral?
Agradeço desde já

-
NathBitencourt
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 13, 2014 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Man Utd » Qui Jun 19, 2014 01:22
por Man Utd » Qui Jun 19, 2014 01:22
Olá

Vc derivou errado, a derivada é :
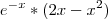
A)
Veja que

é sempre positiva , então resta-nos investigar a função

que é decrescente no intervalo x<0 , crescente no intervalo 0<x<2 e novamente decrescente no intervalo x>2.
B) candidatos a máximo e minimo relativos, veja que x=0 e x=2 anulam a primeira derivada então são pontos criticos , faça o teste da segunda derivada para saber quais são pontos de máximo e de minimo.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Máximos e Mìnimos Derivadas
por brunojorge29 » Sex Set 30, 2011 10:00
- 1 Respostas
- 1451 Exibições
- Última mensagem por LuizAquino

Sáb Out 01, 2011 13:55
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADAS] Máximos e Mínimos
por Jefferson_mcz » Seg Jun 10, 2013 11:28
- 0 Respostas
- 1656 Exibições
- Última mensagem por Jefferson_mcz

Seg Jun 10, 2013 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Mínimos e Máximos, dificuldade em determinar derivadas
por letciabr7 » Qua Jun 10, 2015 17:44
- 1 Respostas
- 2405 Exibições
- Última mensagem por nakagumahissao

Ter Out 06, 2015 09:05
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo 1] Máximos e mínimos de uma função
por LuisLemos » Qua Jul 27, 2016 21:27
- 4 Respostas
- 6861 Exibições
- Última mensagem por LuisLemos

Qui Jul 28, 2016 00:49
Cálculo: Limites, Derivadas e Integrais
-
- [maximos e minimos] Função de duas variaveis
por amigao » Ter Nov 26, 2013 19:41
- 0 Respostas
- 866 Exibições
- Última mensagem por amigao

Ter Nov 26, 2013 19:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 determine:
determine: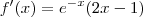 . Só que a partir dai eu não consegui fazer mais nada! Depois de chegar em casa eu continuei a tentar e não conseguia resolver. Depois de desistir eu fui procurar no google para ver se achava algo em relação a isso e eu só acho questões usando integrais (matéria que a gente não viu ainda).
. Só que a partir dai eu não consegui fazer mais nada! Depois de chegar em casa eu continuei a tentar e não conseguia resolver. Depois de desistir eu fui procurar no google para ver se achava algo em relação a isso e eu só acho questões usando integrais (matéria que a gente não viu ainda).



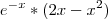
 é sempre positiva , então resta-nos investigar a função
é sempre positiva , então resta-nos investigar a função  que é decrescente no intervalo x<0 , crescente no intervalo 0<x<2 e novamente decrescente no intervalo x>2.
que é decrescente no intervalo x<0 , crescente no intervalo 0<x<2 e novamente decrescente no intervalo x>2.


 , avisa que eu resolvo.
, avisa que eu resolvo.

