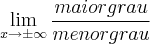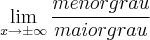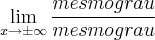Caro G-Schimitt-JR,
Sempre que vc for resolver limites com divisões de polinômios que tendem no infinito, observe o seguinte:
1º Caso, se houver uma divisão de polinômio que tende para mais ou menos infinito, e tiver o maior grau em cima (ou seja, no numerador) então o limite será
+ infinito, ou - infinito. No seu caso, ele será menos infinito.
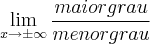 2º Caso
2º Caso, se houver uma divisão de polinômio que tende para mais ou menos infinito, e tiver o maior grau em baixo (ou seja, no denominador) então o limite será
zero. POis, a função de baixo cresce muito rápido, levando o limite pra zero.
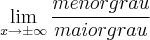 3º Caso
3º Caso, se houver uma divisão de polinômio que tende para mais ou menos infinito, e tiver o mesmo grau em cima (ou seja, no numerador) e em baixo (ou seja, no denominador) então
o limite será o coeficiente de maior grau do polinômio.
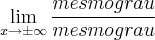
Espero que esse macete possa lhe ajudar.
Obs: Não esqueça de prestar atenção nos sinais