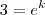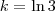por marinalcd » Sex Ago 09, 2013 15:19
por marinalcd » Sex Ago 09, 2013 15:19
Um amigo me pediu ajuda nessa questão, mas não consegui ajudá-lo, pois Estou com muita dificuldade nesse tipo de questão. Estou me complicando ao tentar resolver questões desse tipo através de equações diferenciais.
Alguém pode me dar uma luz?
"Uma população de bactérias cresce de acordo com o modelo de Malthus. Se a população inicial era de 1.000 bactérias e ao final de uma hora, ela era de 3.000 bactérias, de quanto a população aumentou ao fim de duas horas?"
Obrigada!
-
marinalcd
- Colaborador Voluntário

-
- Mensagens: 143
- Registrado em: Sex Abr 27, 2012 21:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Man Utd » Dom Jun 15, 2014 17:40
por Man Utd » Dom Jun 15, 2014 17:40
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1863 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
-
- equacoes diferenciais
por Thais Bomfim » Qua Dez 12, 2012 01:58
- 2 Respostas
- 2193 Exibições
- Última mensagem por Thais Bomfim

Qua Dez 12, 2012 14:02
Equações
-
- Equações Diferenciais
por sergio2205 » Qua Mar 06, 2013 13:27
- 1 Respostas
- 1737 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 15:14
Equações
-
- Equações Diferenciais
por FernandaOliveira » Dom Ago 25, 2013 20:42
- 1 Respostas
- 1666 Exibições
- Última mensagem por FernandaOliveira

Qua Ago 28, 2013 16:41
Equações
-
- Equações Diferenciais
por FernandaOliveira » Dom Ago 25, 2013 20:52
- 1 Respostas
- 1218 Exibições
- Última mensagem por young_jedi

Seg Ago 26, 2013 16:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



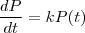



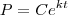
 :
:
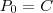

 :
: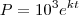
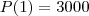 :
: