Bom, estou estudando sistemas de equações diferenciais e acabei de ver a parte com autovalores complexos, onde usamos Euler para resolver.
Esta parte consegui entender. A questão é, aprendi para casos com autovalores imaginários puros, mas como faço quando, ao estudar algum sistema,
encontrar autovalores da forma a + bi? Não consegui achar nenhum exemplo para me ajudar nessa dúvida, tentei pensar sozinha, mas na hora de usar
Euler estou me enrolando e não consigo fazer. Alguém tem algum exemplo de como faço nesses casos?
Obrigada!
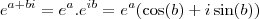
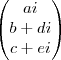
![\begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right]](/latexrender/pictures/ac8f5d03462ba94735ddda40c0817030.png "\begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}
+ i
\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}\left[cos(gt)+ isen(gt) \right]")
![\left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2}](/latexrender/pictures/ebbb561f367ec6243c6b84b379e8e730.png "\left[ \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.cos(gt)- \begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{1} + \left[\begin{pmatrix}
a \\
d\\
e\\
\end{pmatrix}.{e}^{f}.cos(gt) + \begin{pmatrix}
0\\
b\\
c\\
\end{pmatrix}.{e}^{f}.sen(gt)\right]{c}_{2}")
.
, 
e para 
, 
.
e 
, monte a função e substitua 
por 
.
