Dá pra ver de cara que x tem que ser diferente de zero pois não pode existir divisão por zero.
Mas pode existir o limite de x->0+ e de x->0-
Assintotas:
Só resolver o limite de x tentendo a -infinito e +infinito. Se este f(x) existir e tender a uma constante, estas serão as assintotas horizontais.
Depois achar os x para f(x) tentendo a +infinito e -infinito. Se existir, estas serão as assintotas verticais.
Vc saber encontrar os pontos críticos:
a derivada primeira, se f'(x) = 0 existir, estes serão os pontos máximos ou minimos locais.
a derivada segunda se f''(x) = 0 encontramos os pontos de inflexão. Estes pontos delimitam mudanças de concavidades.
Com estes pontos críticos x e os x onde são -infinito e +infinito, coloque em ordem cada um destes pontos.
-infinito < critico1 < ... < criticoN < +infinito
Marque cada um destes pontos criticos e trace fracamente cada assintota no gráfico.
Para sabermos se as regiões, delimitadas por cada ponto critico, são crescentes ou decrescentes:
escolha valores entre cada ponto crítico e resolva f'(x) onde x=criticoN. Se o sinal desta solução for negativo, então a função é decrescente nesta região. Se for positivo é crescente.
Se escolher um dos pontos criticos dessa f'(x), não poderemos definir se cresce ou decresce porque o resultado de f'(x) será zero.
Para sabermos se as regiões, delimitadas por cada ponto critico, tem convidade para cima ou para baixo:
escolha valores entre cada ponto crítico e resolva f''(criticoN). Se o sinal desta solução for negativo, então a concavidade é para baixo nesta região. Se for positivo é para cima.
Os exatos pontos criticos dessa f''(x) não podem dizer se a concavidade é crescente ou decrescente.
Se escolher um dos pontos criticos encontrados na f''(x)=0, não poderemos definir se cresce ou decresce porque o resultado de f''(x) será zero.
Regra da cadeia:
[ f(g(x)) ]' = f'(g(x))*g'(x)
A matéria de integral é muito grande para passar aqui.
http://pt.wikipedia.org/wiki/IntegralEu gostei da explicação deste site:
http://pessoal.sercomtel.com.br/matemat ... tegral.htm



![\[e^-x^2/2\] \[e^-x^2/2\]](/latexrender/pictures/5356bb430ce96ac06739c2ecd3bf5688.png)
![\[-x. e^(-x^2/2)\] \[-x. e^(-x^2/2)\]](/latexrender/pictures/65433b95655679edbcb130cb74bced45.png)
![\[e^-x^2/2 \] \[e^-x^2/2 \]](/latexrender/pictures/b109493ccfa3340576b272edcd2ea8dd.png) * (x² - 1)
* (x² - 1)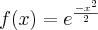
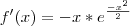
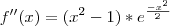

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)