1º

Eu resolvi substituindo o limite primeiramente, ficou:
 que diante de meus conhecimentos (corriga se eu estiver errado) é igual a
que diante de meus conhecimentos (corriga se eu estiver errado) é igual a  . No entanto o gabarito simplifca a equação deixando o X em evidencia resultando em
. No entanto o gabarito simplifca a equação deixando o X em evidencia resultando em  . Se eu estiver correto, porque simplificar a equação?
. Se eu estiver correto, porque simplificar a equação?2º Nao consegui resolver a raiz de limite
![\lim_{x->\infty} \sqrt[]{x} \lim_{x->\infty} \sqrt[]{x}](/latexrender/pictures/b51b152a21547dcc545f8994b6e3b589.png)
Tudo que eu sei sobre as operações básicas entre limites é que podemos multiplicar, dividir, somar e subtrair limites somente com jogo de sinais, a unica inderterminação seria
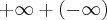 e
e  .
. alguma objeção?
obrigado pela atenção! ph


 por
por uma indeterminação do tipo
uma indeterminação do tipo  que, no limite
que, no limite 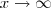 , resulta em
, resulta em  e se obtém a resposta do limite com as parcelas restantes.
e se obtém a resposta do limite com as parcelas restantes.
 e
e  . É claro que
. É claro que 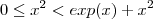 .Logo para qualquer que seja
.Logo para qualquer que seja  . E além disso , o limite de ambas funções no infnito é
. E além disso , o limite de ambas funções no infnito é  , por exemplo. Se tomarmos o limite
, por exemplo. Se tomarmos o limite ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.