 por blaze » Qua Mai 07, 2014 17:36
por blaze » Qua Mai 07, 2014 17:36
Quero resolver a seguinte integral imediata ou quase imediata
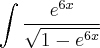
Com o Microsoft Mathematics posso facilmente saber o resultado, mas não o percebo. Sei que não é necessário usar o método de substituição ou integrar por partes, mas por mais voltas que dê não consigo fazer isto apenas com o inverso da derivada.
-
blaze
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 07, 2014 17:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Mai 07, 2014 19:24
por Russman » Qua Mai 07, 2014 19:24
Use o método de substituição. Imagino que você esteja integrando a função com relação a

.
Faça
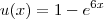
. Desse modo,
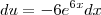
e , portanto, a integral se simplifica para
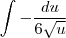
que tem primitiva conhecida.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por blaze » Qua Mai 07, 2014 19:29
por blaze » Qua Mai 07, 2014 19:29
Obrigado

-
blaze
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 07, 2014 17:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Mai 07, 2014 19:55
por Russman » Qua Mai 07, 2014 19:55
Bons estudos. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Próximo Número...?
por Molina » Sáb Jun 21, 2008 17:44
- 8 Respostas
- 8862 Exibições
- Última mensagem por Rafael Dias

Sáb Ago 30, 2008 22:31
Desafios Fáceis
-
- número de elementos
por sinuca147 » Qui Mai 14, 2009 04:43
- 4 Respostas
- 6185 Exibições
- Última mensagem por sinuca147

Dom Mai 17, 2009 17:14
Conjuntos
-
- apóstolos no número
por lieberth » Qui Jun 18, 2009 18:42
- 2 Respostas
- 1761 Exibições
- Última mensagem por Molina

Sex Jun 19, 2009 08:41
Álgebra Elementar
-
- apóstolos no número
por lieberth » Sex Jun 19, 2009 19:19
- 0 Respostas
- 1107 Exibições
- Última mensagem por lieberth

Sex Jun 19, 2009 19:19
Números Complexos
-
- Número inteiro
por thadeu » Qua Nov 18, 2009 19:27
- 0 Respostas
- 921 Exibições
- Última mensagem por thadeu

Qua Nov 18, 2009 19:27
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
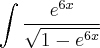

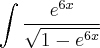

 .
.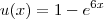 . Desse modo,
. Desse modo, 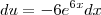 e , portanto, a integral se simplifica para
e , portanto, a integral se simplifica para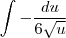



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)