 por ilane » Sex Abr 25, 2014 22:51
por ilane » Sex Abr 25, 2014 22:51
\int_{-1}^{1} xe^x^2 dx
tenho que calcular essa integral e cheguei na seguinte resposta gostaria de saber se está certa ou não
\int_{-1}^{1} e ^x^2 x ^x^2 . dx \approx1.50033+0,691773i
-
ilane
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Ter Abr 08, 2014 10:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: quimica
- Andamento: cursando
 por e8group » Sáb Abr 26, 2014 00:12
por e8group » Sáb Abr 26, 2014 00:12
Numero complexo ??
A integral é essa
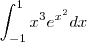
? Se for nem precisa fazer contas , a resposta é zero . A teoria abaixo justifica isto .
Fixemos

e definamos
![f : [-a,a] \mapsto \mathbb{R} f : [-a,a] \mapsto \mathbb{R}](/latexrender/pictures/5f54e28a1094d492221c71c6497580d4.png)
contínua (ou número de descontinuidade finito )[hipótese para garanti a integrabilidade de f ] e além disso suponha

uma função ímpar , isto é
![f(x) = - f(-x) \forall x \in [-a,a] f(x) = - f(-x) \forall x \in [-a,a]](/latexrender/pictures/6ae07197d28f59849fad10a691c8a1e7.png)
. Agora veja ...
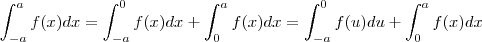
.
Como f é impar

. Fazendo

, temos

e os limites de integração

.Assim ,

. E portanto ,

.
Conclusão : o resultado de integrais definidas (cujos limites de integração são simétricos um do outro ) em relação a função impares (que satisfaz as condições de ser integrável = ser contínua ou contínua por partes ) será
sempre zero .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4614 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4582 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4346 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Qua Ago 17, 2011 22:33
- 2 Respostas
- 2844 Exibições
- Última mensagem por ewald

Qui Ago 18, 2011 00:54
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Integral funçao trigonometrica
por ewald » Sáb Ago 20, 2011 17:20
- 2 Respostas
- 2869 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 21:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



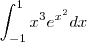 ? Se for nem precisa fazer contas , a resposta é zero . A teoria abaixo justifica isto .
? Se for nem precisa fazer contas , a resposta é zero . A teoria abaixo justifica isto .  e definamos
e definamos ![f : [-a,a] \mapsto \mathbb{R} f : [-a,a] \mapsto \mathbb{R}](/latexrender/pictures/5f54e28a1094d492221c71c6497580d4.png) contínua (ou número de descontinuidade finito )[hipótese para garanti a integrabilidade de f ] e além disso suponha
contínua (ou número de descontinuidade finito )[hipótese para garanti a integrabilidade de f ] e além disso suponha  uma função ímpar , isto é
uma função ímpar , isto é ![f(x) = - f(-x) \forall x \in [-a,a] f(x) = - f(-x) \forall x \in [-a,a]](/latexrender/pictures/6ae07197d28f59849fad10a691c8a1e7.png) . Agora veja ...
. Agora veja ... 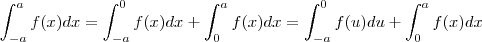 .
.  . Fazendo
. Fazendo  , temos
, temos  e os limites de integração
e os limites de integração  .Assim ,
.Assim , . E portanto ,
. E portanto , .
.